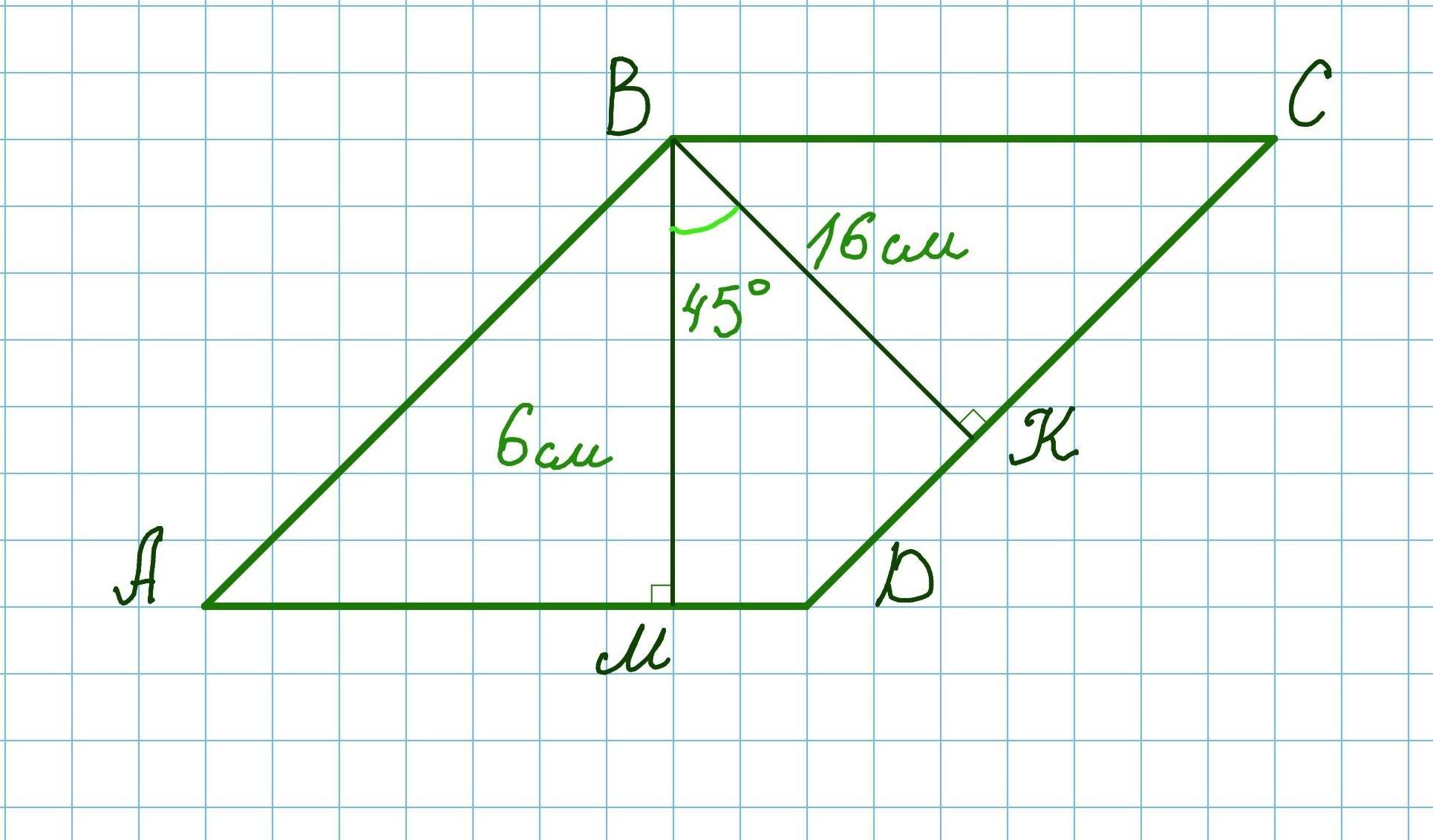
Висоти ВМ і ВК паралелограма ABCD дорівнюють 6 см і 16 см відповідно, а кут МВК дорівнює 45°. Знайдіть площу паралелограма АВCD.

Ответ:

Площа паралелограма АВСD дорівнює 96√2 см²

Объяснение:

ABCD - паралелограм, ВМ і ВК - висоти. ВМ⟂AD, ВК⟂CD.

ВМ=6см, ВК=16см. ∠МВК=45°.

ЗНАЙТИ: площу паралелограма АВCD.

Площа паралелограма рівна добутку сторони на висоту проведену до неї.

S=a•h

1)Оскільки ВМ - висота ABCD, то BM⟂BC. ∠MBC=90°, отже ∠СВК=∠МВС-∠МВК=90°-45°=45°.

2)Розглянемо прямокутний △СВК(∠К=90°, BK⟂CD).

Так як сума гострих кутів прямокутного трикутника дорівнює 90°, то ∠ВСК=90°-∠СВК=90°-45°=45°.

∠ВСК=∠СВК тому △СВК - рівнобедрений: ВК=КС=16см.

3)За теремою Піфагора знайдемо гіпотенузу ВС.

ВС²=ВК²+КС²=16²+16²=2×16², тоді ВС=16√2 см.

У паралелограма протилежні сторони рівні, тому AD=BC=16√2 см.

4)Площа паралелограма: S=a•h=AD•BM=16√2•6=96√2см²