Вища математика )
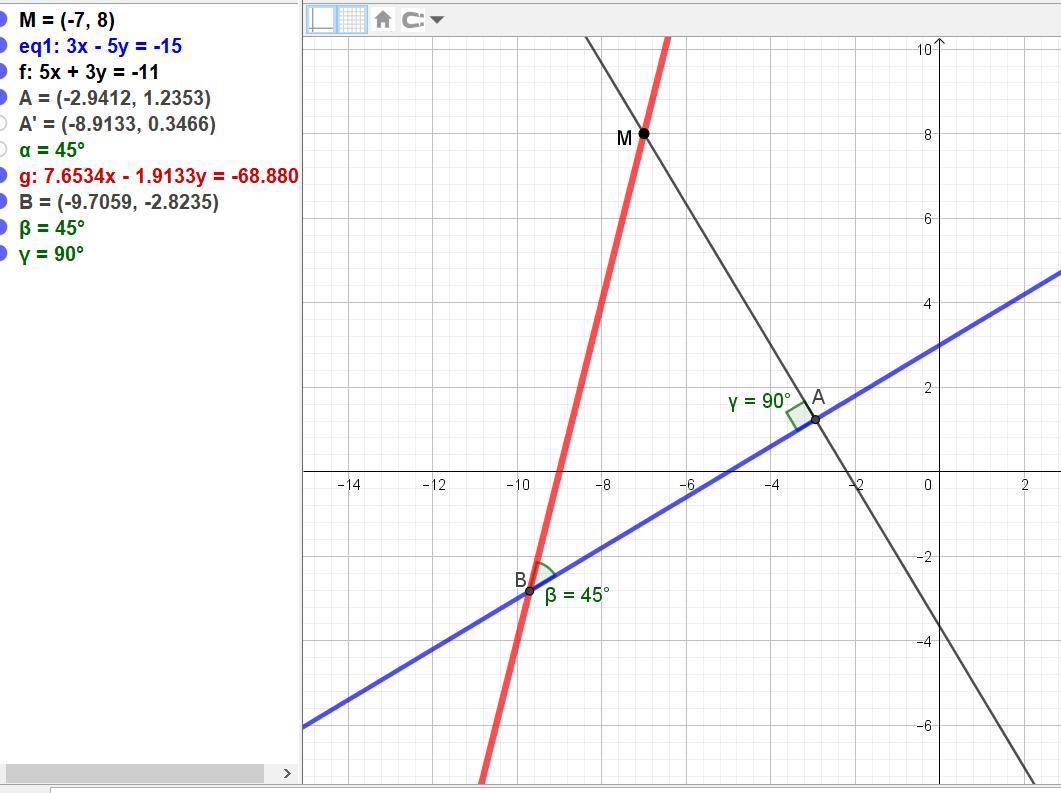
1. Складіть рівняння прямих ,які проходять через точку М(-7;8) під кутом 45° до прямої 3х-5у+15=0
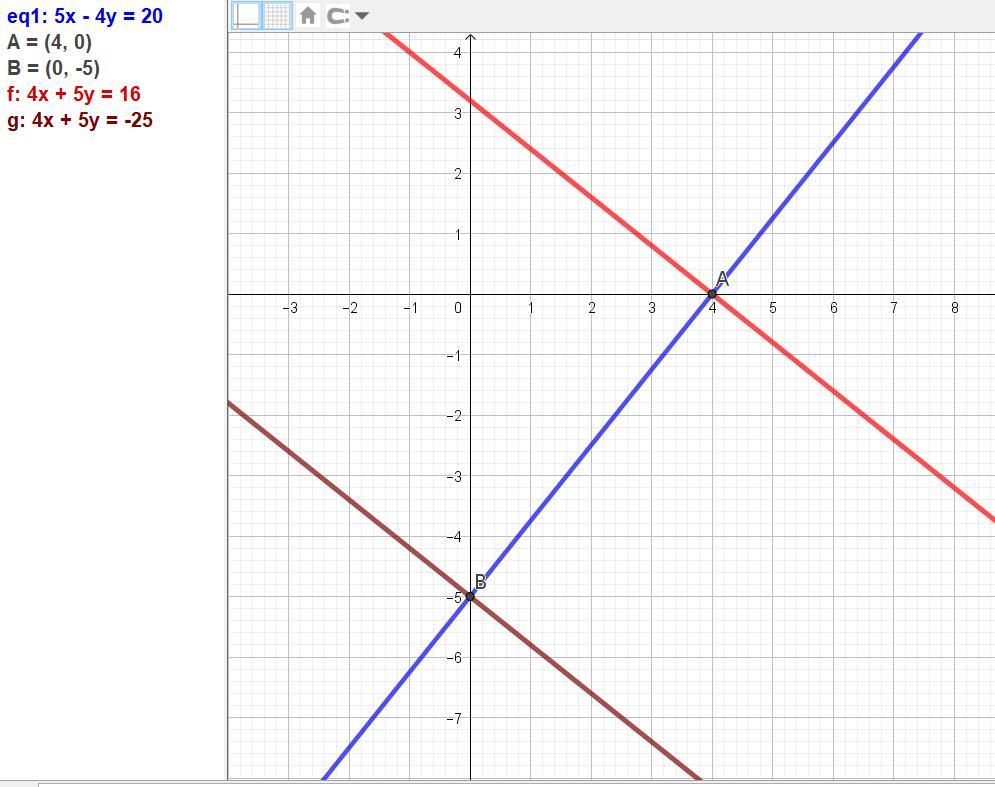
2. Знайдіть рівняння двох перпендикулярів до прямої 5х-4у-20=0 у точках перетину її з осями координат

1) Надо применить формулу тангенса суммы углов.

Уравнение заданной прямой выразим относительно у.

у = (3/5)x + 5.

Здесь к = (3/5) = tg α.

Тангенс угла 45 градусов равен 1.

tg(α + β) = (tg α + tg β)/(1 - tg α*tg β) = ((3/5) + 1)/(1 - (3/5)*1) = (8/5)/(2/5) = 4.

Получаем уравнение у = 4х + b, подставим координаты точки М.

8 = 4*(-7) + b, отсюда b = 8 + 28 = 36.

Ответ: у = 4х + 36.

2) У перпендикулярной прямой в общем виде Ах + Ву + С = 0 коэффициенты нормального вектора меняются -В и А.

Получаем уравнения 4х + 5у + С = 0.

Теперь находим заданные точки пересечения с осями.

Точка А (пересечение с осью Ох, при этом у = 0) х = 20/5 = 4.

А(4; 0).

Точка В (пересечение с осью Оу, при этом х = 0) у = 20/(-4) = -5.

В(0; -5.

Подставляем координаты точки А: 4*4 + 5*0 + С = 0, С = -16.

Подставляем координаты точки В: 4*0 + 5*(-5) + С = 0, С = 25.

Ответ: (А) 4х + 5у - 16 = 0,

           (В) 4х + 5у + 25 = 0.