Алгебра, вопрос задал svetlanaguzevat , 1 год назад

Вирішати 1 приклад....​

Приложения:

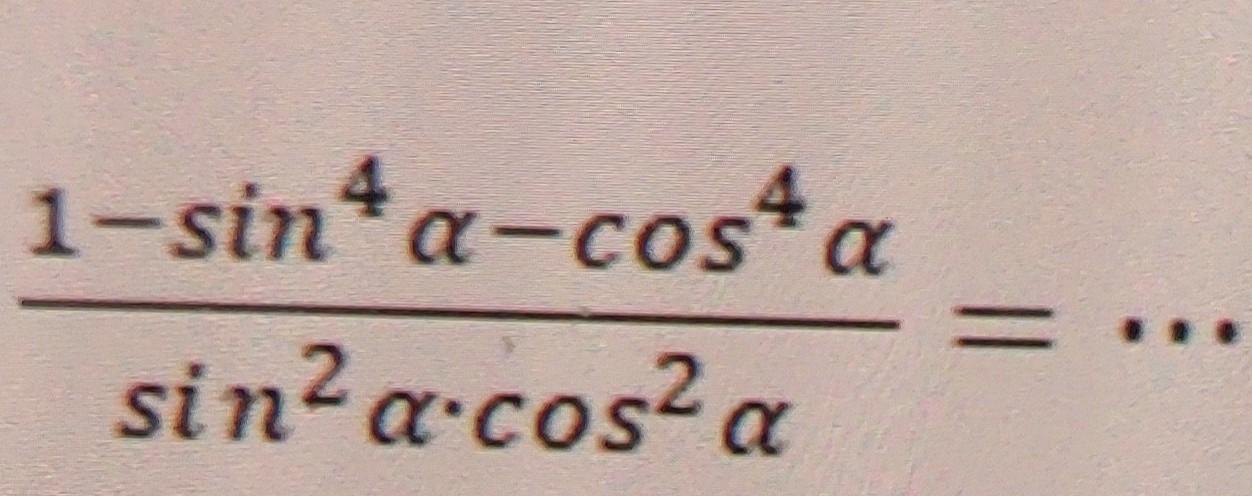
Ответы на вопрос

Ответил Universalka
1

\displaystyle\bf\\\frac{1-Sin^{4} \alpha -Cos^{4} \alpha }{Sin^{2}\alpha \cdot Cos^{2} \alpha } =\frac{Sin^{2}\alpha +Cos^{2} \alpha -Sin^{4} \alpha -Cos^{4} \alpha }{Sin^{2}\alpha \cdot Cos^{2} \alpha } =\\\\\\=\frac{(Sin^{2}\alpha -Sin^{4} \alpha)+(Cos^{2}\alpha -Cos^{4} \alpha) }{Sin^{2}\alpha \cdot Cos^{2} \alpha } =\\\\\\=\frac{Sin^{2} \alpha \cdot(1-Sin^{2} \alpha )+Cos^{2}\alpha \cdot(1-Cos^{2}\alpha ) }{Sin^{2} \alpha \cdot Cos^{2} \alpha } =

\displaystyle\bf\\=\frac{Sin^{2} \alpha \cdot Cos^{2} \alpha +Cos^{2}\alpha \cdot Sin^{2} \alpha }{Sin^{2} \alpha \cdot Cos^{2} \alpha } =\frac{2Sin^{2} \alpha Cos^{2}\alpha }{Sin^{2}\alpha Cos^{2} \alpha } =2

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика, 1 год назад
Нехай Данило має набір з k карток, занумерованих числами від 1 до k. Знайдіть усі значення k, при яких він може вибрати  рівно 10 пар, для яких сума чисел у кожній  парі дорівнює 100. ​
Английский язык, 1 год назад
Допоможіть!!!!!!!!!!!!!!! ​
Английский язык, 1 год назад
Допоможіть!!:( будь ласка, швидко!
Українська література, 1 год назад
охарактеризувати головного героя твору П. Попельського "Сліпий Музикант"...
Геометрия, 6 лет назад
ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ОЧЕНЬ СРОЧНО!!
История, 6 лет назад
напишите пожалуйста, план по захвату польши ?​