Математика, вопрос задал godlev2006 , 1 год назад

Вирішіть тригонометричне рівняння. Розпишіть ваше рішення.

Приложения:

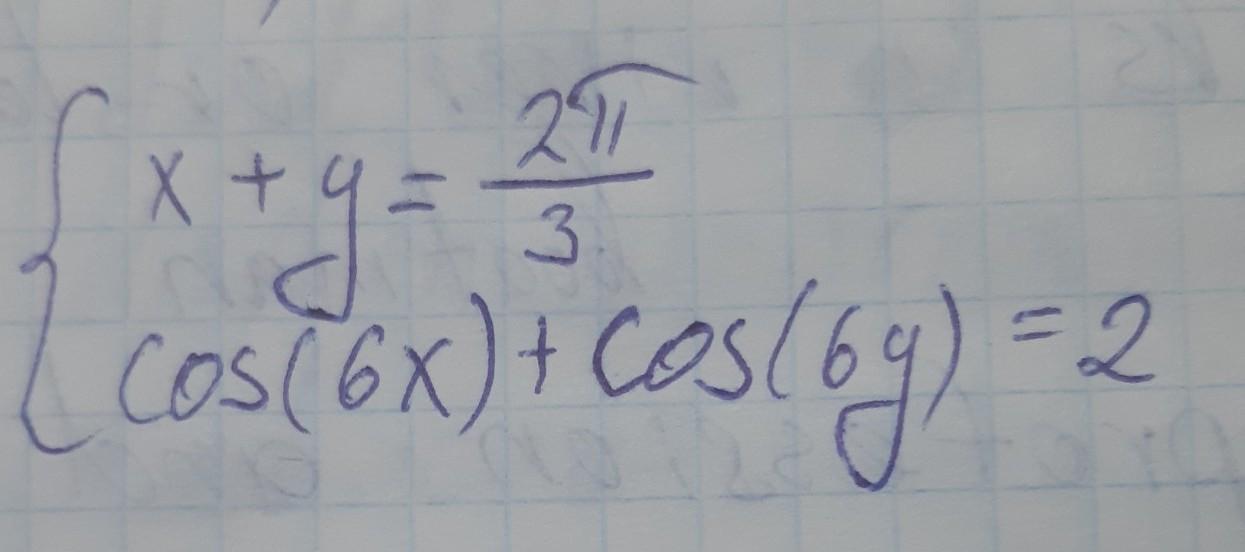
Ответы на вопрос

Ответил FaerVator

Ответ:

( x ; y ) = ( πn/3 ; (2π - πn)/3 ) , n∈Z

Объяснение:

$\left. \begin{cases} { \displaystyle x + y = \frac{2\pi}{3}; } \\ { \cos(6x) + \cos(6y) = 2 ; } \end{cases} \right. \left. \begin{cases} { \displaystyle y = \frac{2\pi}{3} - x; } \\ { \cos(6x) + \cos(6y) = 2;} \end{cases} \right.$

В первом уравнении мы выразили у через х , а второе уравнение распишем по формуле суммы косинусов:

$\displaystyle \sf cos \alpha + cos \beta = 2cos\left( \frac{ \alpha + \beta }{2} \right) \cdot cos \left( \frac{ \alpha - \beta }{2} \right)$

Тогда мы имеем:

$\displaystyle 2 \cos\left( \frac{6x + 6y}{2} \right) \cdot \cos\left( \frac{6x - 6y}{2} \right) = 2|:2 \\ \\ \cos(3x + 3y) \cdot \cos(3x - 3y) = 1$

Подставим у , которую мы выразили в начале:

$\bf \displaystyle \cos \bigg(3x + 3\left( \frac{2 \pi}{3} - x\right) \bigg) \cdot \cos\bigg(3x - 3\left( \frac{2 \pi}{3} - x\right) \bigg) = 1$

$\cos(3x + 2\pi - 3x) \cdot \cos(3x - 2\pi + 3x) = 1 \\ \\ \cos2\pi \cdot \cos(6x - 2\pi) = 1 \\ \\ \cos(6x - 2\pi) = 1 \\ \\ \cos6x = 1 \\ \\ 6x = 2 \pi n|:6 \\ \\ \boldsymbol{x = \frac{ \pi n}{3} , n\in Z }$