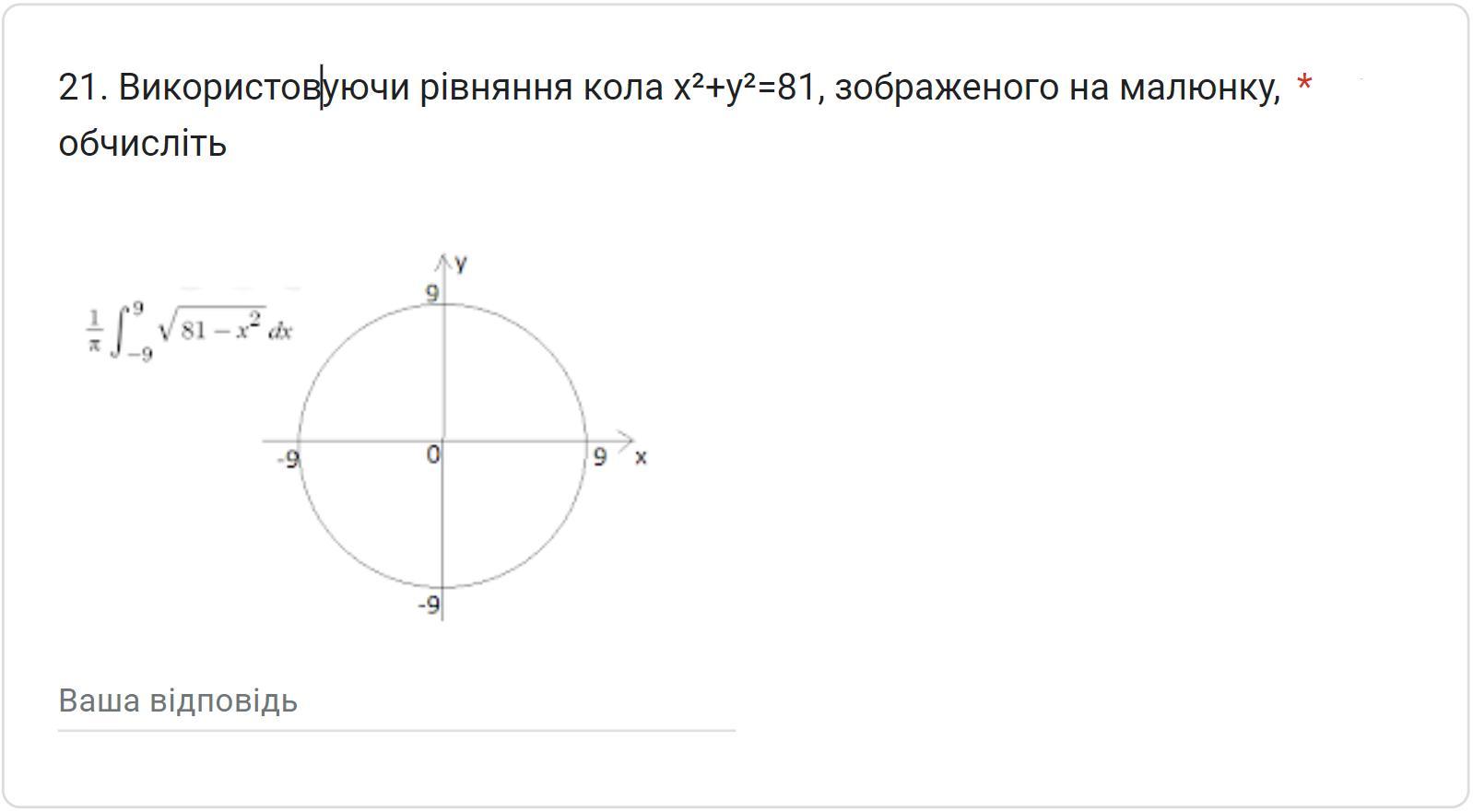
Використовуючи рівняння кола x²+y²=81, зображеного на малюнку, обчисліть: (завдання на фото)
бажано щоб були зоч якісь пояснення як то зробити так як мені потрібно розуміння як таке завдання виконувати.

Ответ:

40,5

Пошаговое объяснение:

Воспользовавшись уравнением окружности x² + y² =81  , изображенном на рисунке вычислить

Воспользуемся геометрической интерпретацией определенного интеграла.

Рассмотрим подынтегральную функцию

Так как арифметический квадратный корень есть число неотрицательное, то

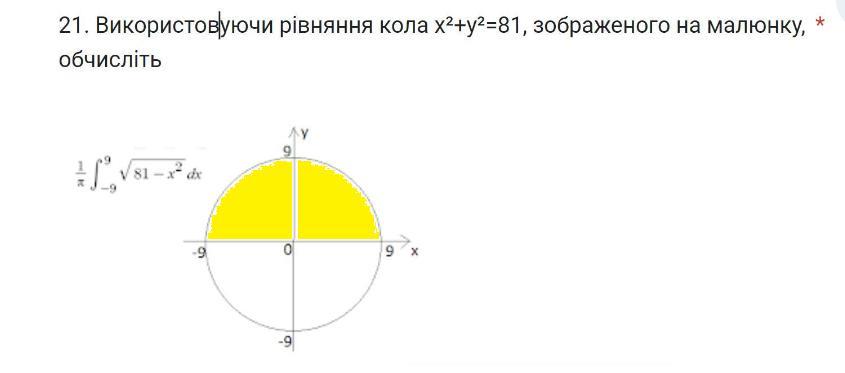
Тогда определенный интеграл равен площади полукруга ( рисунок во вложении)

Площадь круга определяется по формуле S =πR².

По условию уравнение окружности x² + y² =81. Тогда R = 9  и площадь круга, ограниченной этой окружностью , будет

S =π · 9² = 81 π.

Тогда площадь полукруга будет равна

Значит,

#SPJ1