Алгебра, вопрос задал fctdgsygfdhngfxzgsac , 11 месяцев назад

Використовуючи метод інтегрування частинами, обчислити.

Приложения:

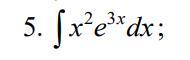
Ответы на вопрос

Ответил NNNLLL54

1

Ответ:

Метод интегрирования по частям применяем два раза .. Формула :

$\bf \displaystyle \int u\cdot dv=uv-\int v\cdot du$

$\bf \displaystyle \int x^2\cdot e^{3x}\, dx=\Big[\ u=x^2\ ,\ du=2x\, dx\ ,\ dv=e^{3x}\, dx\ ,\ v=\frac{1}{3}\, e^{3x}\ \Big]=\\\\\\=\frac{1}{3}\, x^2\cdot e^{3x}-\frac{2}{3}\int x\cdot e^{3x}\, dx=\Big[\ u=x\ ,\ du=dx\ ,\ dv=e^{3x}\, dx\ ,\\\\\\v=\frac{1}{3}\, e^{3x}\ \Big]\ \ =\ \frac{1}{3}\, x^2\cdot e^{3x}-\frac{2}{3}\cdot \Big(\frac{1}{3}\, x\cdot e^{3x}-\frac{1}{3}\int e^{3x}\, dx\Big)=\\\\\\=\frac{1}{3}\, x^2\cdot e^{3x}-\frac{2}{9}\, x\cdot e^{3x}+\frac{2}{9}\cdot e^{3x}+C$

Приложения:

fctdgsygfdhngfxzgsac: спасибо большое)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Немецкий язык, 11 месяцев назад

твір про українську кухню на німецькій мові для 7 класу, люди допоможіть будь ласка...

Українська література, 11 месяцев назад

СРОЧНО!!! Установіть відповідність між художніми засобами та їхнім прикладами: 1) епітет 2) персоніфікація 3) гіпербола 4) риторичне звертання 5) синекдоха а) вражі ляхи б) гей, поїхав...

Физика, 11 месяцев назад

1. Третю частину часу свого руху автомобіль їхав з швидкістю 90 км/год, а решту часу з швидкістю 60KM / год .Визначити середню швидкість руху автомобіля.

Українська мова, 11 месяцев назад

Чому дієприкметники подідяються на активни і пасивни...

Физика, 6 лет назад

помогите пжжжжж, нужен не только ответ, но и решение ...

Математика, 6 лет назад

2 2/9+5/6 допоможіть зробити приклад!!!! Потрібно здати сьогодні?!!! Даю 10 балів!!!!?