Виконати завдання на фото № 78, 79, 82, 86, 87

Ответы на вопрос
Ответ:
Объяснение:
78. Рассмотрим ∆АВД и ∆СВД.
У них: 1) ВД — общая;
2) угол АДВ = углу СДВ (по условию);
3) АД= СД (по условию);
Значит, ∆АВД=∆СВД (по двум сторонам и углу между ними).
ч.т.д.
79. Рассмотрим ∆АВД и ∆СВД.
У них: 1) ВД - общая.
2) угол АДВ = углу СВД (по условию);
3) АД=ВС (по условию).
Значит, ∆АВД=∆СВД (по двум сторонам и углу между ними).
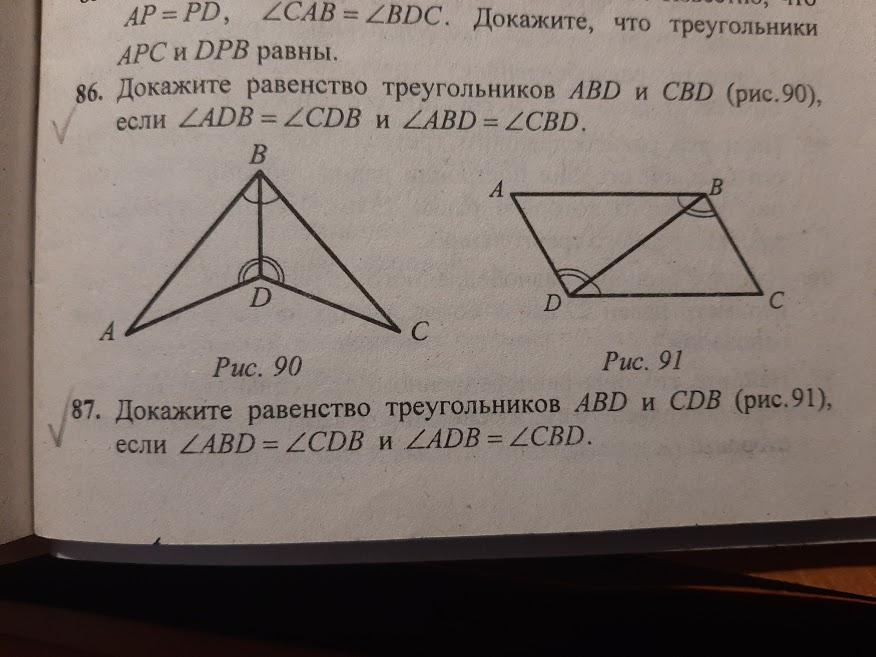
86. Рассмотрим ∆АВД и ∆СВД.
У них: 1) ВД - общая;
2) угол АВД = углу СВД (по условию);
3) угол ВДА = углу ВДС (по условию);
Значит, ∆АВД=∆СВД (по стороне и прилежащим к ней углам).
87. Рассмотрим ∆АВД и ∆СВД.
У них: 1) ВД - общая;
2) угол АВД= углу СДВ (по условию);
3) угол АДВ = углу СВД (по условию);
Значит, ∆АВД=∆СВД (по стороне и прилежащим к ней углам)
78. ΔADB = ΔCDB по двум сторонам (AD = CD, а также общая сторона BD) и углу между ними (∠ADB = ∠CDB), то есть по первому признаку равенства треугольников.
79. ΔADB = ΔCDB по двум сторонам (AD = BC, а также общая сторона BD) и углу между ними (∠ADB = ∠CBD), то есть по первому признаку равенства треугольников.
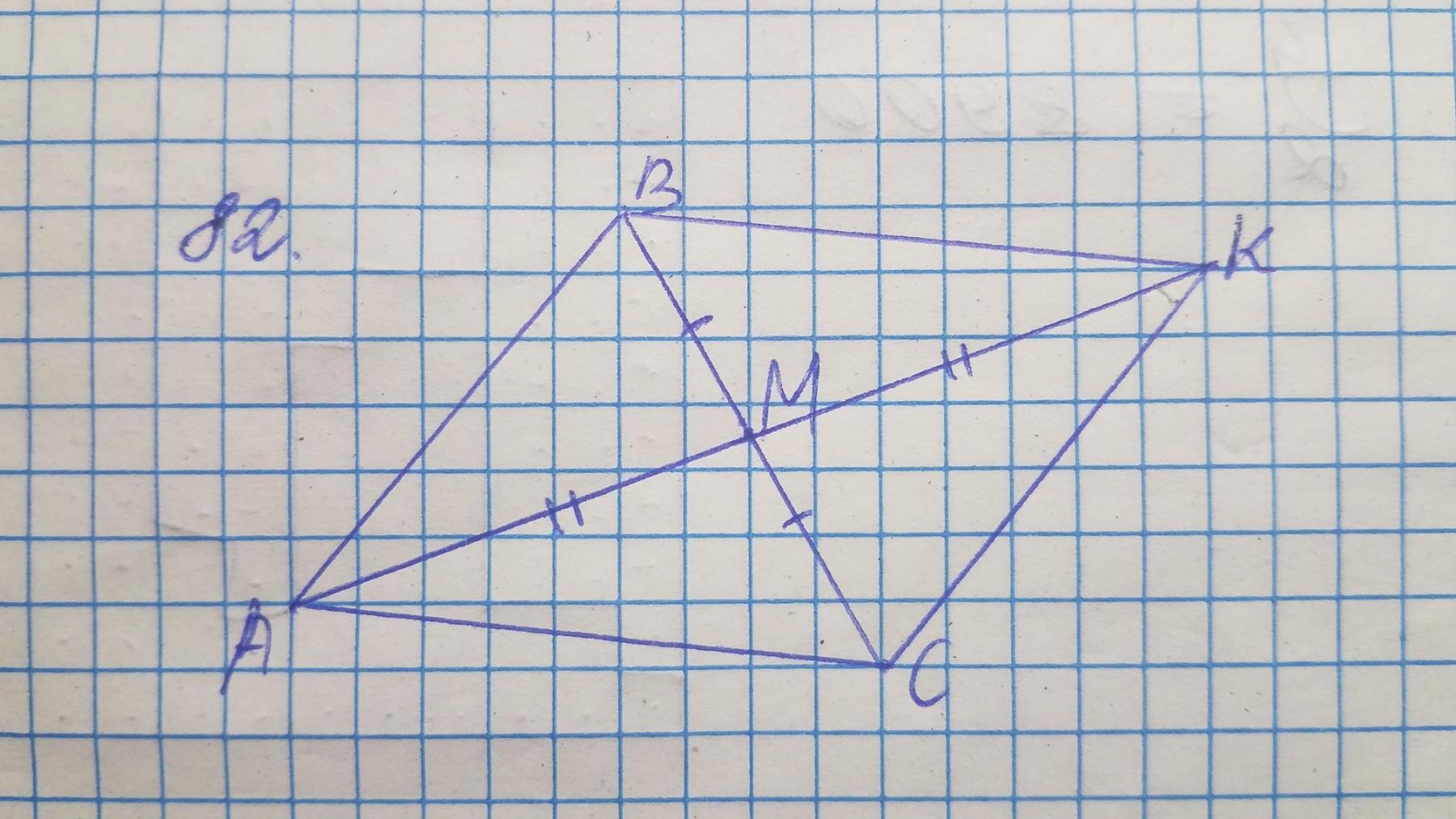
82. ΔACM = ΔKBM по двум сторонам (BM = MC, AM = MK) и углу между ними (∠BMK = ∠AMC, так как эти углы вертикальные), то есть по первому признаку равенства треугольников. Рисунок к задаче на фото.
86. ΔADB = ΔCDB по стороне (общая сторона BD) и двум прилежащим углам (∠ABD = ∠CBD, ∠ADB = ∠CDB), то есть по второму признаку равенства треугольников.
87. ΔADB = ΔCDB по стороне (общая сторона BD) и двум прилежащим углам (∠ABD = ∠CDB, ∠ADB = ∠CBD), то есть по второму признаку равенства треугольников.