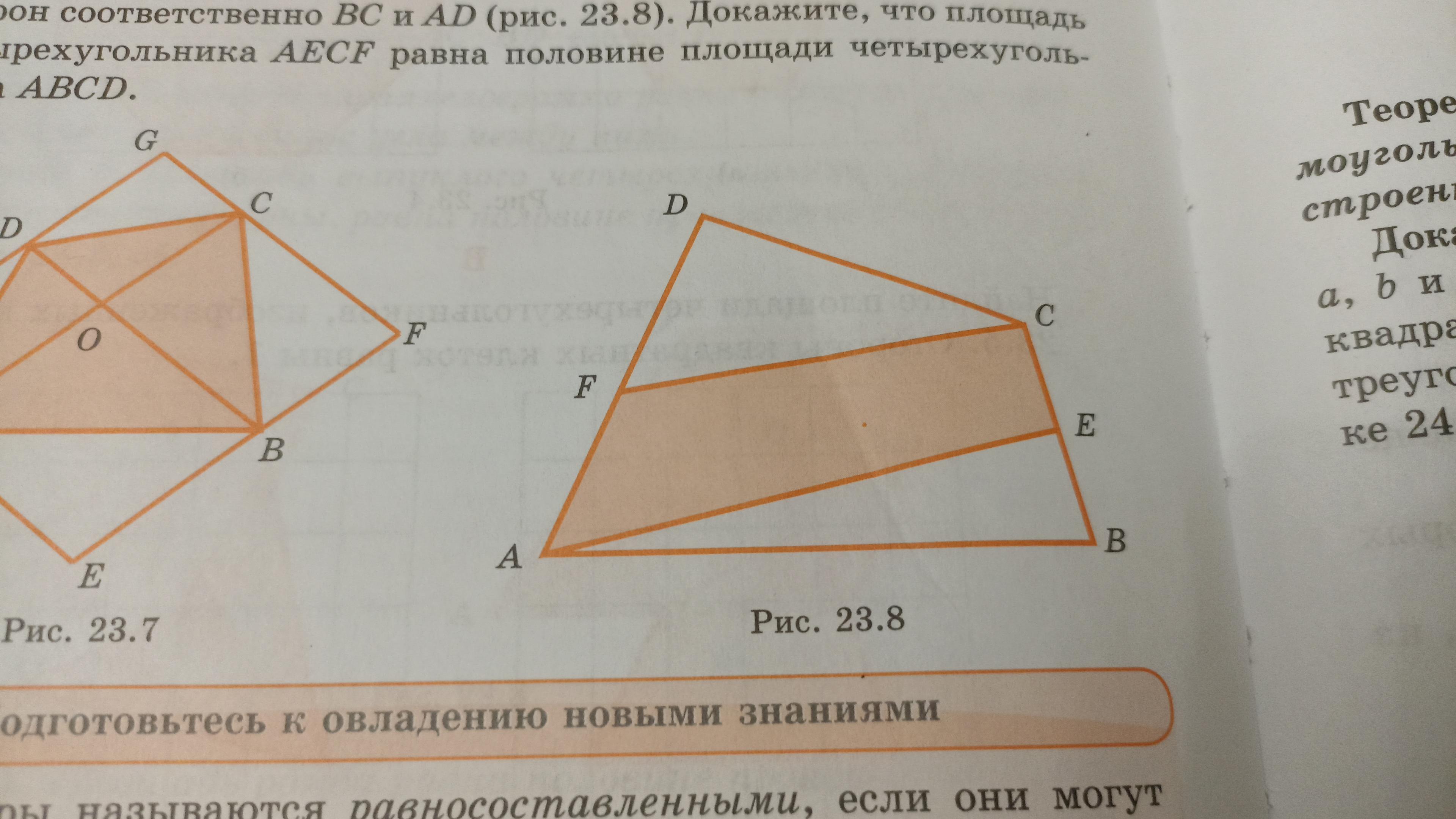
В выпуклом четырехугольнике abcd точки E и F — середины сторон соответственно BC и AD. Докажите, что площадь четырехугольника AECF равна половине площади четырехугольника ABCD

Проведем диагональ AC. Получим треугольник ACD, где CF -медиана и треугольник BAC, где АЕ -медиана Медиана треугольника делит его на два равновеликих треугольника. Следовательно треугольник FCD= треугольнику FCA, а треугольник САЕ= треугольнику ЕАВ Так как площадь АDCB=сумме площадей треугольников FDC, FCA, CAE, EAB, то площадь АFCD равна половине площади АDCB.