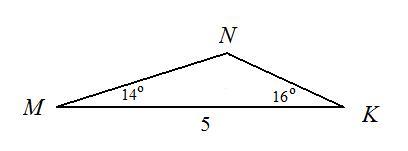
В треугольнике MNK ∠M=14°, ∠K=16°, MK=5. Найдите радиус описанной около этого треугольника окружности

Нужно знать:

1) сумма углов треугольника равна 180°;

2) sin150° = sin(180° - 30°) = sin30° = 1/2 = 0,5;

3) теорема синусов: стороны треугольника пропорциональны синусам противоположных углов и это отношение равно 2R:

                               a/sinα = b/sinβ = c/sinγ = 2R,

где а, b, c - стороны треугольника, α, β и γ - его углы, R - радиус описанной окружности.

Поэтому:

См. рисунок.

∠N = 180° - (∠м + ∠К) = 180 - (14° + 16°) = 150°, значит,

МК/sinN = 2R, R = MK/(2sinN) = 5/(2 · 0,5) = 5/1 = 5.

Ответ: 5.