В треугольнике CDE <E=76, <D=66, EK-биссектриса треугольника. Докажите, что КС>DK
Ответы на вопрос
Ответил KuOV
0
Сумма углов треугольника равна 180°, значит
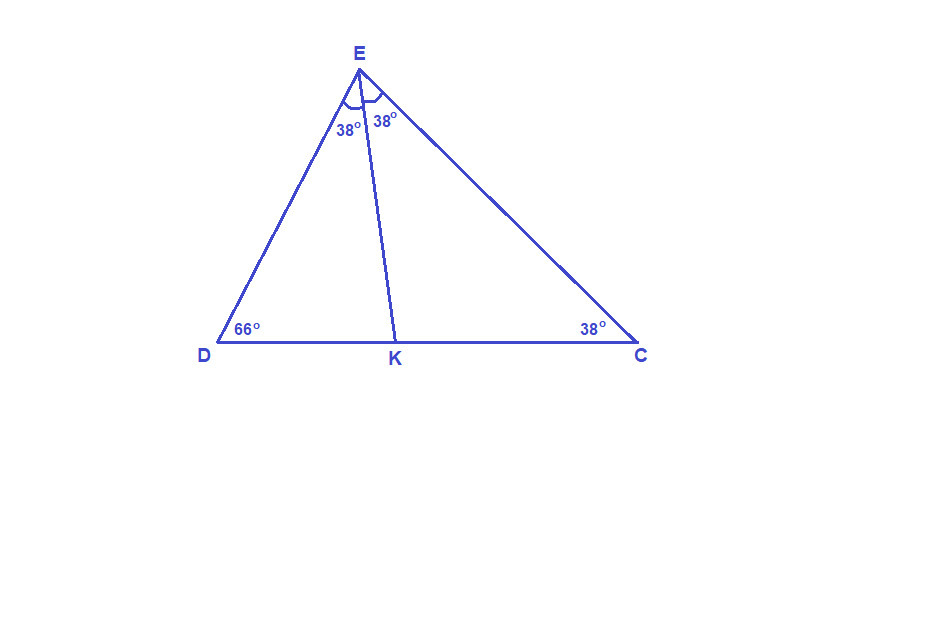
∠DCE = 180° - (∠EDC + ∠CED) = 180° - (66° + 76°) = 180° - 142° = 38°
∠DEK = ∠CEK = 1/2 ∠DEC = 1/2 · 76° = 38°
Значит ΔЕКС - равнобедренный с основанием ЕС, КС = КЕ.
В треугольнике против большего угла лежит большая сторона.
ΔDEK: DK < КЕ,
КЕ = КС, значит DK < KC.
Приложения:
Новые вопросы
Русский язык,
2 года назад
Русский язык,
2 года назад
Математика,
9 лет назад
Информатика,
9 лет назад
Математика,
9 лет назад