В треугольнике АВС высота СД проведена из вершины прямого угла. Катет СЕ равен 6см, ДВ-3,6см. Найдите площадь треугольника АВС.Помогите пожалуйста и начертите если несложно
Ответы на вопрос
Ответил ludmilaksenija2005
4
Ответ:
24 см^2
Объяснение:
АВС ; <С=90 градусов ; СD-высота
DB=3,6 cм
Катет СВ=6 см
Найти :S(ABC)
Решение :
Тр-к ВDC:
По теореме Пифагора :
СD=корень (СВ^2-DB^2)=
=корень (6^2-3,6^2)=корень (36-12,96)=
=корень (23,04)=4,8 см
СD^2=DB×AD
4,8^2=3,6×AD
23,04=3,6×AD
AD=23,04:3,6=6,4 см
AB=DB+AD=3,6+6,4=10 cм
S=1/2×AB×CD=1/2×10×4,8=24 cм^2
Приложения:
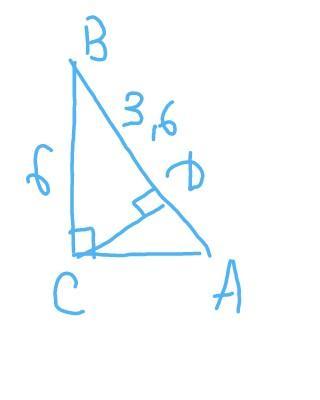
ludmilaksenija2005:
В условии опечатка ВЕ. Решала ВС
То есть СЕ
СПАСИБО вам огромное, очень помогли
♡´・ᴗ・`♡
Новые вопросы
Окружающий мир,
1 год назад
Окружающий мир,
1 год назад
Другие предметы,
6 лет назад
Математика,
6 лет назад