В треугольнике АВС угол А=40 градусов, угол В=100 градусов

а)Докажите, что треугольник АВС - равнобедренный, и укажите его основание.

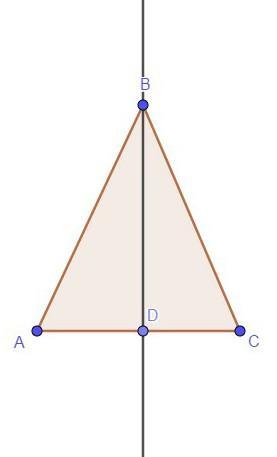
б)Отрезок ВН - высота даного треугольника. найдите углы, на которые она делит угол АВС

Помогите пожалуйста!!! С решением и рисунком

а) Доказательство:

По теореме о сумме углов в треугольнике:

∠С = 180° - ∠A - ∠B = 180° - 40° - 100° = 40°.

Если ∠С = 40°, то ∠С = ∠A. Из этого следует, что △ABC - равнобедренный (BA = BC), что и требовалось доказать.

б) Решение:

Выше мы уже доказали, что △ABC - равнобедренный (BA = BC).

В равнобедренном треугольнике высота, проведённая из вершины угла, противоположного основанию (в данном случае из ∠B), является также его биссектрисой.

Биссектриса делит угол пополам. Отсюда ∠ABH = ∠CBH. А если ∠B = 100°, то ∠ABH = ∠CBH = 100° / 2 = 50°.

Ответ: 50°.