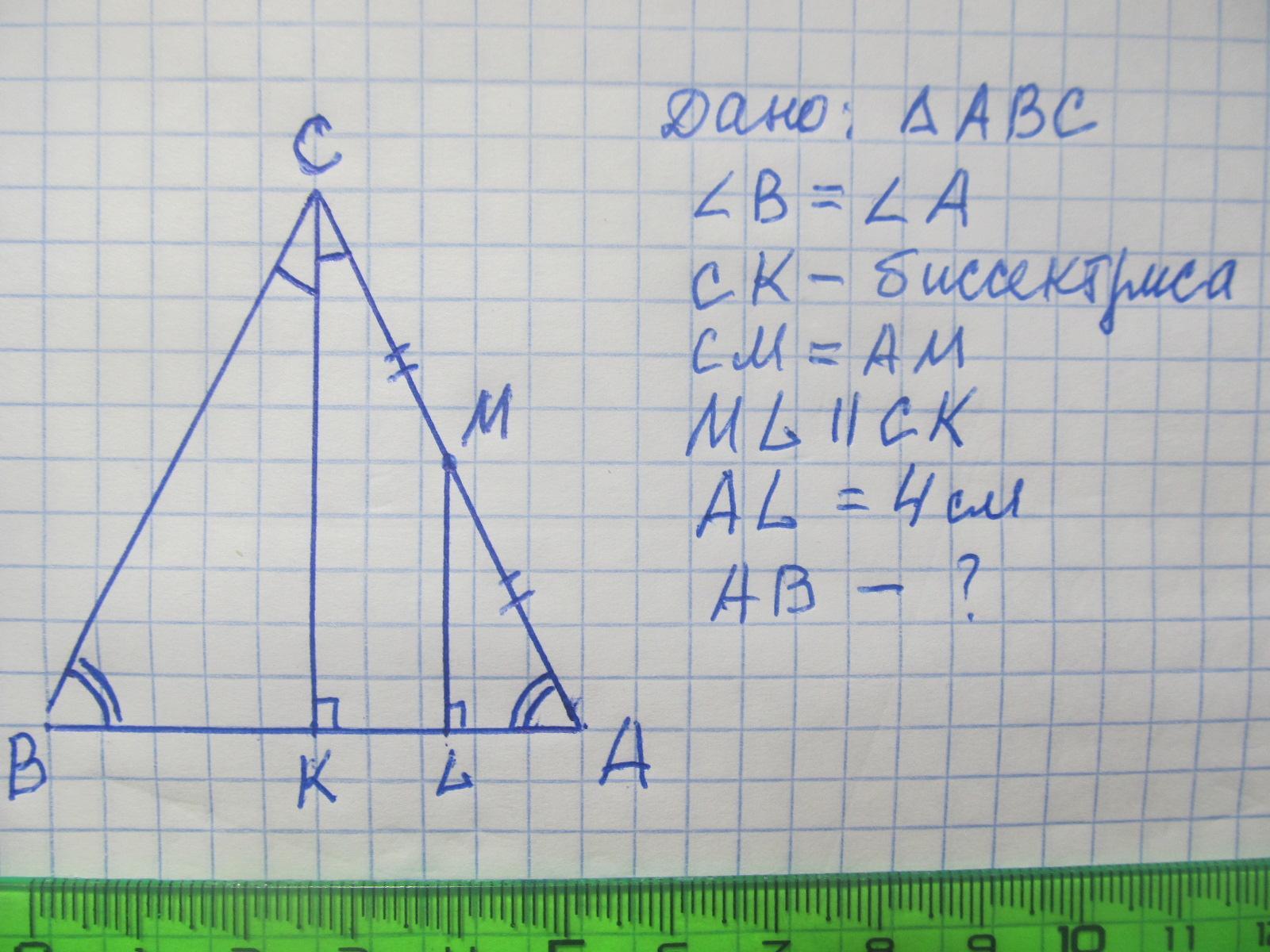
В треугольнике АВС углы ВАС и АВС равны. Из середины стороны АС проведена прямая параллельная биссектрисе СК. Она пересекает сторону АВ в точке L. AL=4см. Найдите АВ. (4б.)
Ответы на вопрос
Ответил Аноним
6
ΔАВС - р/б; СВ=СА т.к. углы при его основании равны.
∠А=∠В по условию.
СК - биссектриса, медиана и высота; ⇒ ВК=АК.
Рассм. ΔАСК; СМ=АМ по условию; ML║CK по условию ⇒
ML - средняя линия ΔАСК по признаку средней линии.
⇒ KL=LA=4 см. (или по Фалесу)
АК=2*4=8 см.
АВ=2АК по свойству биссектрисы р/б Δ, проведенной из вершины.
АВ=8*2=16 см - это ответ.
Приложения:
Аноним:
См. выше. Попросите, чтобы написали сначала Вам, тогда появится чат и Вы сможете писать, не имея пока 1000 решений)))
как удалить комментарий и ответ?или только можераторы удаляют
И вопрос и ответ может удалить модератор "по просьбе".
спасиибо
Новые вопросы
Другие предметы,
1 год назад
Математика,
2 года назад
Русский язык,
2 года назад
Алгебра,
7 лет назад