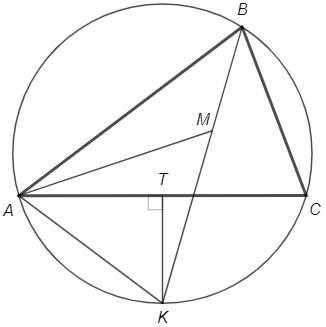
в треугольнике АВС точка М центр вписанной окружности и биссектриса угла АВС пересекает описанную окружность в точке к. найдите длину отрезка МК если cos авс=0,28, ас 30

Центр вписанной окружности M - точка пересечения внутренних биссектрис △ABC

∠AMK =∠BAM+∠ABM =A/2 +B/2 (внешний угол △ABM)

∠CAK=◡CK/2=CBK =B/2

∠MAK =∠CAM+∠CAK =A/2 +B/2

=> ∠AMK=∠MAK => △AKM -р/б, MK=AK

◡AK=B=◡CK => AK=CK (равные дуги - равные хорды)

△AKC -р/б => KT - высота/медиана

AT=AC/2=15

cos(CAK) =cos(B/2) =√((1+cosB)/2) =√(1,28/2) =0,8

(Угол в прямоугольном треугольнике - острый, косинус положительный.)

MK =AK =AT/cos(CAK) =15/0,8 =18,75