в треугольнике авс точка х лежит на стороне ав а точка у лежит на стороне вс. отрезки ау и сх пересекаются в точке з. известно , ау = су и ав=сз. докажите что точки в х з лежат на одной окружности.

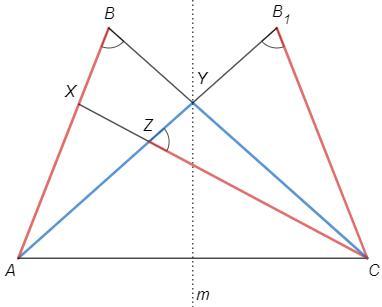
Докажем, что точки B, X, Y, Z лежат на одной окружности.

△AYC - равнобедренный.

Ось симметрии р/б треугольника - серединный перпендикуляр к основанию (m).

Возьмем точку B1 симметричную B относительно m.

∠B=∠B1, AB=CB1 (по построению)

AB=CZ=CB1 => △B1CZ - р/б => ∠B1=∠CZB1

=> ∠CZB1=∠B

Внешний угол четырехугольника BXYZ равен противолежащему внутреннему - четырехугольник вписанный (вершины лежат на одной окружности).