Геометрия, вопрос задал verbinam , 8 лет назад

В треугольнике авс известно, что ас=7, вс=15, угол с=90. Найдите радиус описанной около этого треугольника окружности

Ответы на вопрос

Ответил NataliaBorisevich

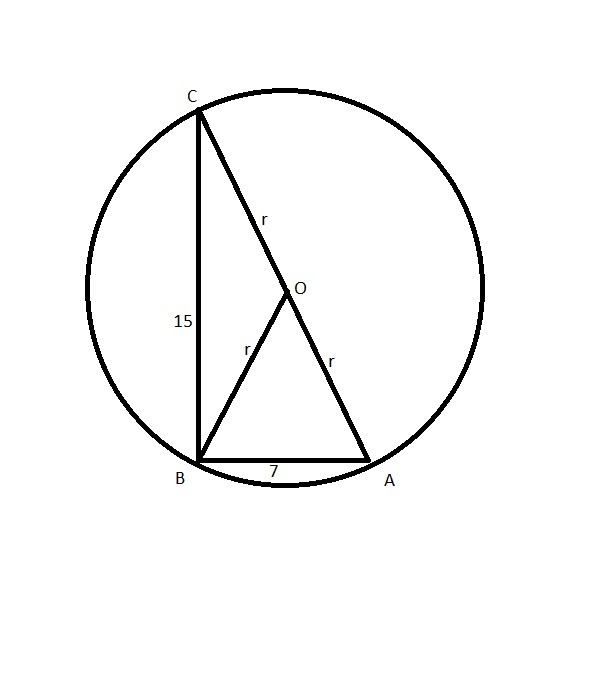
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. ⇒ r = 1/2 гипотенузы.
$AB = sqrt{ AC^{2} + CB^{2} } = sqrt{ 7^{2}+ 15^{2} } = sqrt{49+225} = sqrt{274}$
$r= frac{ sqrt{274} }{2}$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 2 года назад

4. Your friend who _____(come) here the other day ______(seem) very nice. * came/was seeming was coming/seemed came/seemed 5. When I ____(see) the man, he ______(stand) outside the bank. He...

Алгебра, 2 года назад

6(x-y)=6x-6y $25(a - a) = 25$ ...

Литература, 8 лет назад

кто такой Чичиков?Нужны ли Чичиков в России?Сможет ли Росия выйти из тупика блогодаря Чичикову?

Алгебра, 8 лет назад

$(x+4)^{log2 (2x^{2 } -x) } leq 2x^{2}-x$ ...

Обществознание, 9 лет назад

В 2012 году ученые опросили школьников страны Z . Школьники отвечали на вопрос: "Почему важно беречь природу?" Вот результаты опроса: 7% Затрудняюсь ответить 8% Природа - источник творческого...

Химия, 9 лет назад

Sp2 гибридизация атомов углерода имееется в молекулах...