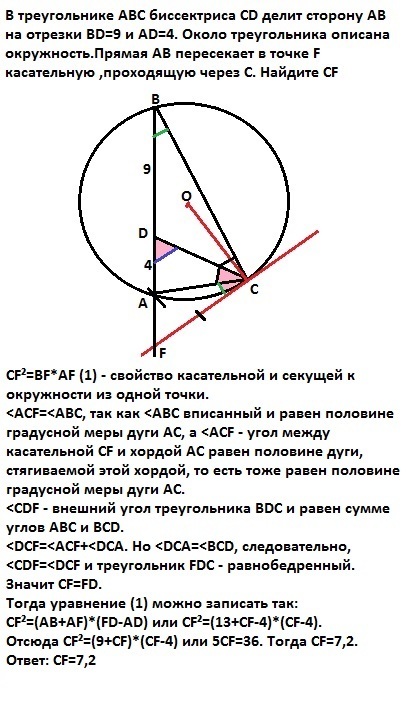
В треугольнике АВС биссектриса СD делит сторону АВ на отрезки ВD=9 и АD=4. Около треугольника описана окружность.Прямая АВ пересекает в точке F касательную ,проходящую через С. Найдите СF

CF²=BF*AF (1) - свойство касательной и секущей к окружности из одной точки.
<ACF=<ABC, так как <ABC вписанный и равен половине градусной меры дуги АС, а <ACF - угол между касательной СF и хордой АС равен половине дуги, стягиваемой этой хордой, то есть тоже равен половине градусной меры дуги АС.
<CDF - внешний угол треугольника ВDC и равен сумме углов АВС и ВСD.
<DCF=<ACF+<DCA. Но <DCA=<BCD, следовательно, <CDF=<DCF и треугольник FDC - равнобедренный. Значит СF=FD.
Тогда уравнение (1) можно записать так:
CF²=(AB+AF)*(FD-AD) или CF²=(13+CF-4)*(CF-4). Отсюда
CF²=(9+CF)*(CF-4) или 5CF=36. Тогда CF=7,2.
Ответ: СF=7,2