в треугольнике авс , ав = ас . медиана к боковой стороне делит высоту проведенную к основанию на отрезки больший из которых равен 8.найдите длину этой высоты
Ответы на вопрос
Ответил Lomoami
0
Медианы АН и ВК треугольника АВС точкой пересечения О делятся в отношении 2:1, считая от вершины ( свойство). АО=8 ⇒ АН=3•8/2=12. Медиана равнобедренного треугольника ( АВ=АС), проведенная из вершины, является его высотой. Следовательно. ∆ АВН - прямоугольный. По т.Пифагора ВН=НС=5. Ѕ(АВС)=АН•ВС:2=8•5=40 ед. площади.
Ответил Senpai908
0
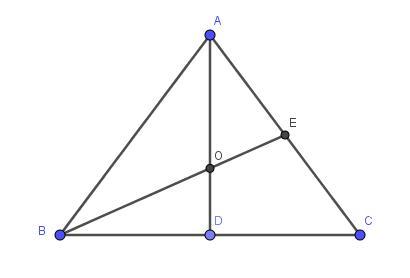
Высота AD, проведенная к основанию BC является биссектрисой и медианой. О - точка пересечения медиан. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, начиная от вершины.
Пусть AO = 2x и OD = x, тогда из условия AO = 8, решим уравнение
2x = 8
x = 4
Тогда OD = 4, следовательно, AD = AO + OD = 8 + 4 = 12
Ответ: 12
Приложения:
Ответил lilyatomach
0
Ответ:
решение представлено на фото
Объяснение:
Приложения:

Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Математика,
7 лет назад
Информатика,
8 лет назад
Алгебра,
8 лет назад