В треугольнике АВС , A =67°, .C =35°, BD – биссектриса угла АВС. Через вершину В

проведена прямая MN и AC. Найдите угол MBD.

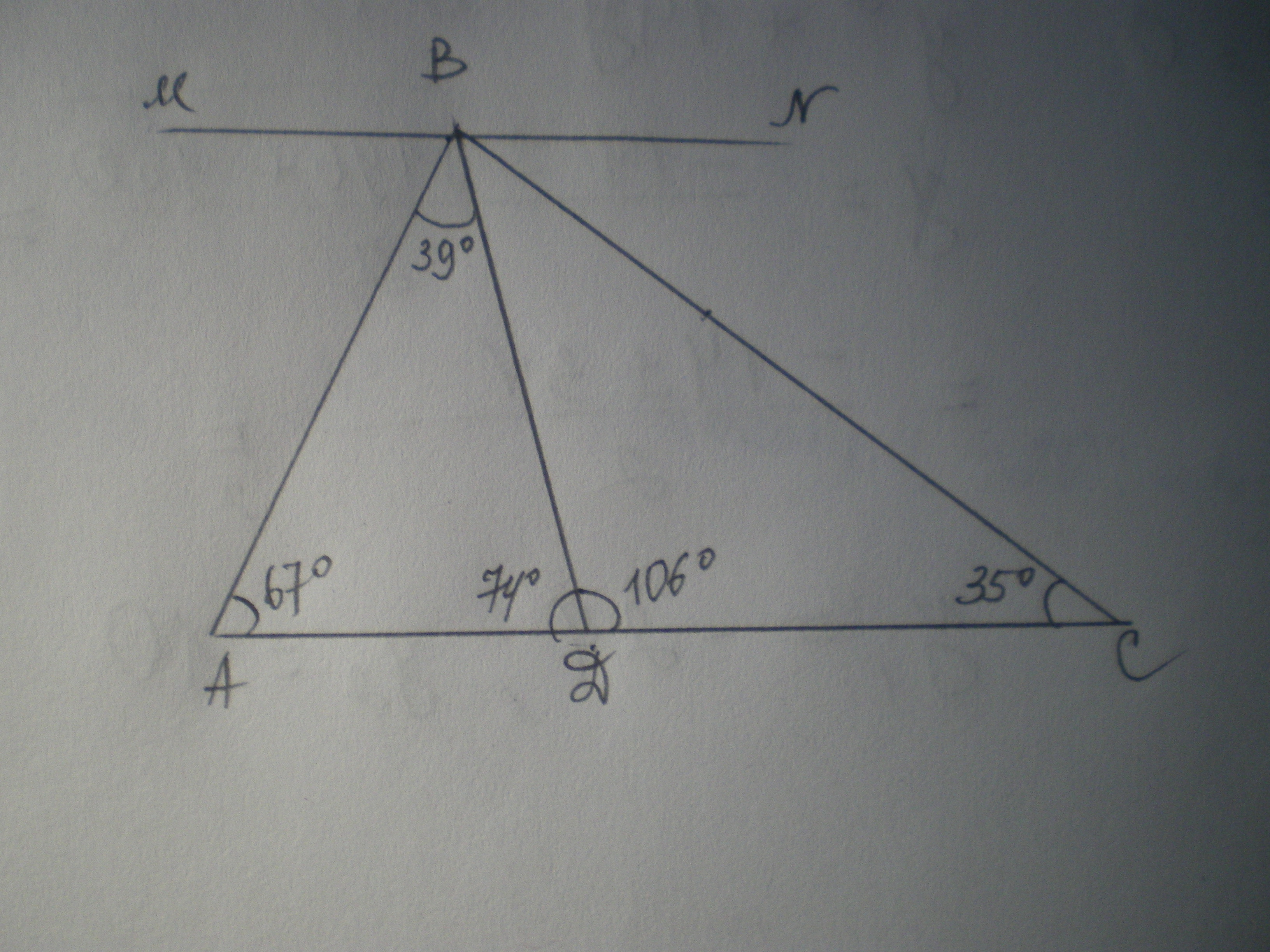
В Δ АВС  ∠A =67°,  ∠C =35°, BD – биссектриса ∠ АВС. Через вершину В  проведена прямая MN ║ AC. Найдите ∠ MBD.

Решение: ∠В=180-67-35=78°

∠АВД=12 ∠В=78:2=39° (по определению биссектрисы)

∠АДВ=180-67-39=74°

∠ВДС=180-74=106° (по свойству смежных углов)

∠МВД=∠ВДС=106° (как внутренние накрест лежащие при АС║MN и секущей ВД)

Ответ: 106°.