В треугольнике ABC угол C равен 120° AB =22корня из 3, найти радиус окружности описанной около этого треугольника
Ответы на вопрос
Ответил siestarjoki
0
Хорда AB делит описанную окружность на две дуги.
∪AB+∪ACB=360°
Вписанный угол С равен половине дуги, на которую опирается.
∪AB= 2∠С =240°
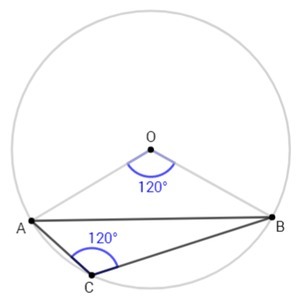
O - центр описанной окружности. Центральный угол AOB равен дуге, на которую опирается.
∠AOB= ∪ACB =360°-∪AB =120°
AO, OB - радиусы описанной окружности. По теореме косинусов
AB^2= 2r^2 -2r^2·cos120° <=> AB^2= 3r^2 <=> r=AB/√3 =22
∪AB+∪ACB=360°
Вписанный угол С равен половине дуги, на которую опирается.
∪AB= 2∠С =240°
O - центр описанной окружности. Центральный угол AOB равен дуге, на которую опирается.
∠AOB= ∪ACB =360°-∪AB =120°
AO, OB - радиусы описанной окружности. По теореме косинусов
AB^2= 2r^2 -2r^2·cos120° <=> AB^2= 3r^2 <=> r=AB/√3 =22
Приложения:
Новые вопросы
Русский язык,
2 года назад
Английский язык,
2 года назад
Математика,
7 лет назад
Информатика,
8 лет назад