в треугольнике ABC угол B тупой, AD медиана треугольника. Докажите, что угол ADC больше угла DAC
Ответы на вопрос
Ответил Mihail001192
29
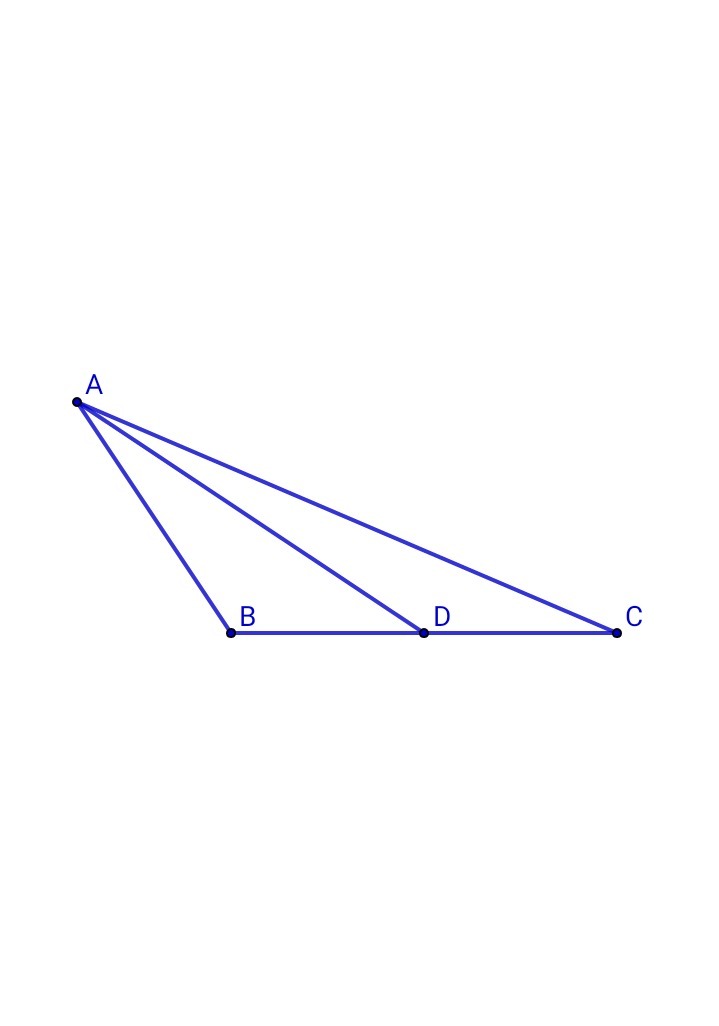
В треугольнике ABC ∠B - тупой, AD - медиана треугольника. Докажите, что ∠ADC > ∠DAC.
=============================================================
В треугольнике против бо'льшей стороны лежит бо'льший угол, а против бо'льшего угла лежит бо'льшая сторона
В ΔАВС: ∠В - тупой - по условию ⇒ АС - наибо'льшая сторона ⇒ АС > ВС
AD - медиана - по условию, BC = 2•CD ⇒ AC > 2•CD
Значит, в ΔACD: АС > CD ⇒ ∠ADC > ∠DAC, что и требовалось доказать.
Приложения:
Новые вопросы