Геометрия, вопрос задал РТУТЬ2006 , 2 года назад

В треугольнике ABC стороны AB и BC равны. Найдите sin A, если AB=25, AC=48.

Ответы на вопрос

Ответил Reideen

Ответ:

$\displaystyle \boldsymbol{\sin \angle A=\frac{7}{25} }$

Объяснение:

1 способ:

Формула Герона (площадь треугольника по трем сторонам): $\displaystyle \boldsymbol{S=\sqrt{p(p-a)(p-b)(p-c)} }$ , где p - полупериметр треугольника ( $\displaystyle p=\frac{a+b+c}{2}$ ), a, b, c - стороны треугольника.
Площадь треугольника через две стороны и угол между ними: $\displaystyle \boldsymbol{S=\frac{1}{2}ab\sin \alpha }$ , где a, b - стороны треугольника, α - угол между ними.

Найдем полупериметр треугольника ΔABC: $\displaystyle \boldsymbol p=\frac{AB+BC+AC}{2} =\frac{25+25+48}{2}=\frac{98}{2} =\boldsymbol{49}$ см.

Тогда с одной стороны площадь треугольника ΔABC равна:

$\displaystyle \boldsymbol{S_{\triangle ABC}}=\sqrt{p(p-AB)(p-BC)(p-AC)} =\\=\sqrt{49(49-25)(49-25)49-48)}= \\\sqrt{49\cdot 24\cdot 24\cdot 1} =7\cdot 24=\boldsymbol{168\;cm^2}$

Но с другой стороны: $\displaystyle \boldsymbol{S_{\triangle ABC}}=\frac{1}{2} \cdot AB\cdot AC\cdot \sin \angle A$ , откуда $\displaystyle \boldsymbol {\sin \angle A} =\frac{2\cdot S_{\triangle ABC}}{AB\cdot AC} =\frac{2\cdot 168}{25\cdot 48} =\boldsymbol{\frac{7}{25} }$ .

2 способ:

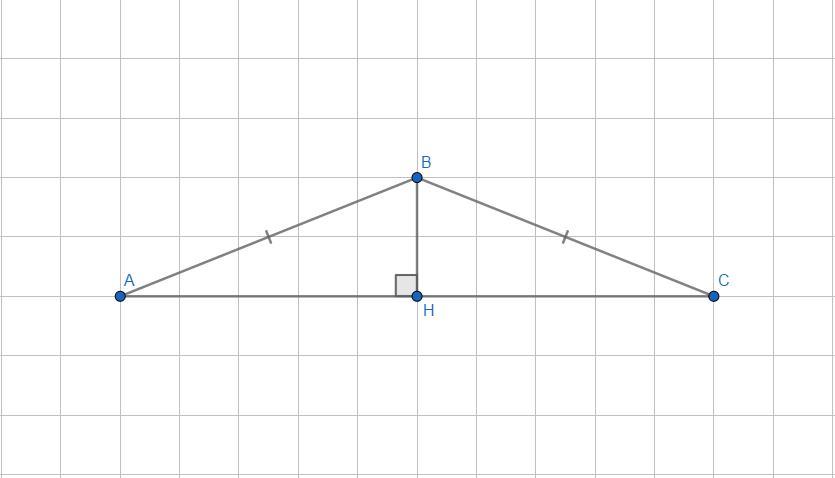
В равнобедренном треугольнике высота является и медианой, и биссектрисой.

Из вершины В опустим высоту ВН (∠AHB=90°). По условию AB=BC, значит, ΔABC - равнобедренный, следовательно, высота BH является медианой, тогда $\displaystyle \boldsymbol{AH=HC=}\frac{AC}{2} =\frac{48}{2} =\boldsymbol{24}$ см.

Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

ΔABH - прямоугольный, т.к. ∠AHB=90°, тогда по т. Пифагора: $AB^2=AH^2+BH^2$ , откуда $\boldsymbol{BH}=\sqrt{AB^2-AH^2}=\sqrt{25^2-24^2} =\sqrt{(25-24)(25+24)}=\sqrt{49}=\boldsymbol{7}$ см.