В треугольнике ABC проведена медиана BM, E — её середина, AE пересекает сторону BC в точке
F. Известно, что CE = MA. Докажите, что EF = BF.

Ответ:

Объяснение: Решение :

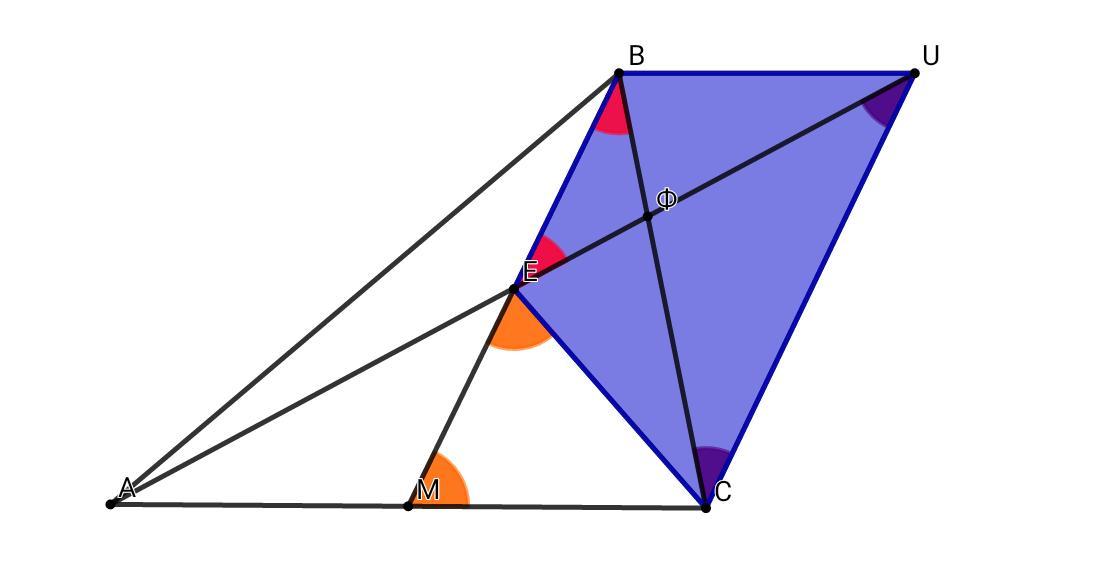
Проведём из точки В прямую BU, параллельную и равную АМ = МС ⇒ ABUM, MBUC - параллелограммы ⇒ АЕ = ЕU

BM || UC , EC∦BU , EC = BU ⇒ BECU - равнобокая трапеция

По свойству равнобокой трапеции: диагонали равнобокой трапеции точкой пересечения делятся на соответственные равные отрезки ⇒ UF = CF , EF = BF , ч.т.д.

АЕ = EU = BC