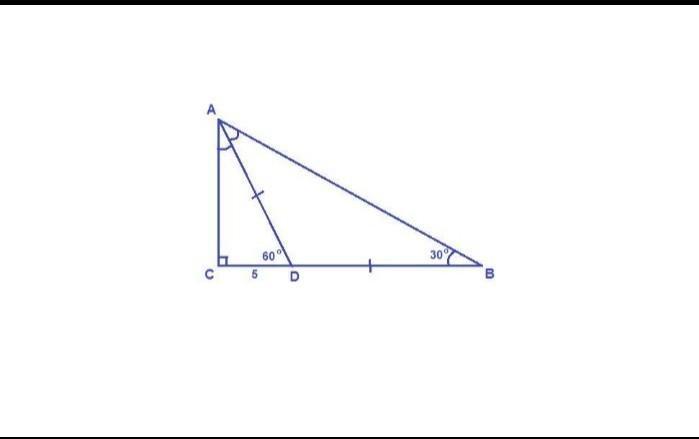
В треугольнике ABC известно, что угол С=90 градусов, угол B=30 градусов. На катете BC отметили точку D такую, что угол ADC=60 градусов. Найдите катет BC, если CD=5 сантиметров.
Ответы на вопрос
Ответ:
Сумма острых углов прямоугольного треугольника равна 90°.
ΔACD: ∠ACD = 90°, ∠ADC = 60°, ⇒
∠DAC = 90° - 60° = 30°.
Против угла в 30° лежит катет, равный половине гипотенузы:
CD = 1/2 AD, ⇒
AD = 2CD = 2 · 5 = 10 см
ΔАВС: ∠АСВ = 90°, ∠В = 30°, ⇒
∠ВАС = 90° - 30° = 60°.
∠BAD = ∠BAC - ∠DAC = 60° - 30° = 30°.
ΔABD: ∠BAD = 30°, ∠ABD = 30°, значит треугольник равнобедренный с основанием АВ.
Тогда BD = AD = 10 см.
ВС = CD + BD = 5 + 10 = 15 см
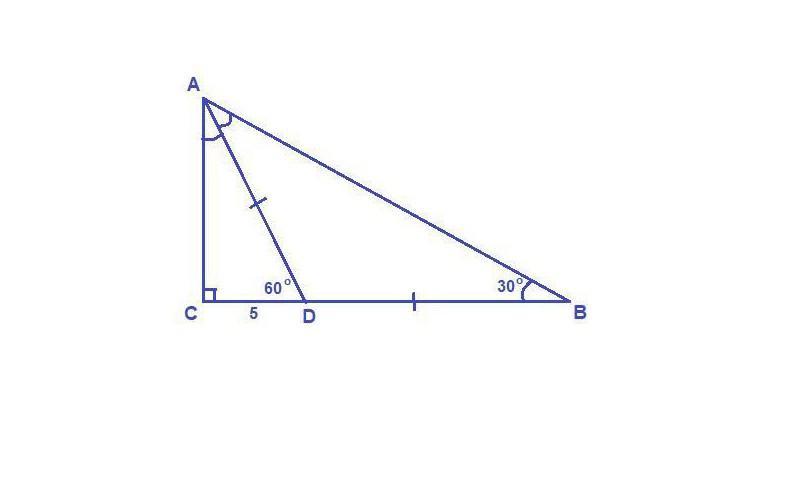
Сумма острых углов прямоугольного треугольника равна 90°.
ДАСD: <ACD = 90°, <ADC = 60°,
<DAC = 90° - 60º = 30°.
ПPOTИB YГЛa B 30° лежит катет, равный половине гипотенузы:
CD = 1/2 AD, =
AD = 2CD = 2 - 5 = 10 см
AABC: ZACB = 90°, ZB = 30°, →
ZBAC = 90° - 30º = 60°.
ZBAD = ZBАС - <DAC = 60º - 30º = 30°.
ДАВD: <BAD = 30°, ZABD = 30°, значит треугольник равнобедренный с
основанием АВ.
Тогда BD = AD = 10 cm.
BC = CD + BD = 5 + 10 = 15 см