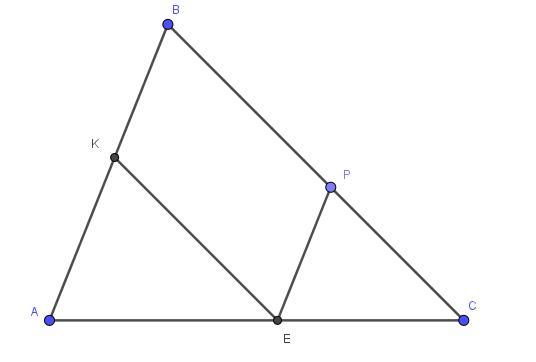
В треугольнике ABC через точку E, которая делит сторону AC в отношении 9:5 , проведены прямые, параллельные AB и BC .Прямая, параллельная AB , пересекает BC в точке P, а параллельная BC пересекает AB в точке K. AB=42
Найдите AK
Найдите PE
Найдите BP : PC
помогите пж дам 50 баллов заранее спасибо
Ответы на вопрос
Ответил Аноним
0
AE : CE = 9 : 5
Рассмотрим треугольники AKE и ABC. У них - общий.
как соответственные. Следовательно, треугольники AKE и АВС подобны (по двум углам). Из подобия треугольников следует пропорциональность соответствующих сторон
Аналогично, (по двум углам).
Приложения:
Новые вопросы