в треугольнике abc 1, 2, 3 внутренние углы треугольника 4,5,6 внешние. Б) угол5+угол6=120. Найдите угол 1 (нужно полное решение) Пожалуйста
Приложения:
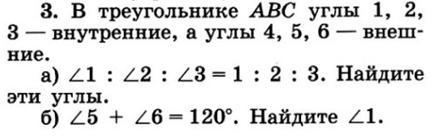
Ответы на вопрос
Ответил Удачник66
3
Ответ:
а) 30°; 60°; 90°; б) В задаче опечатка
Объяснение:
а) ∠1 : ∠2 : ∠3 = 1 : 2 : 3
Всего 6 частей, обозначим углы ∠1 = x; ∠2 = 2x; ∠3 = 3x
Сумма внутренних углов треугольника 180°
∠1 + ∠2 + ∠3 = 180°
x + 2x + 3x = 180°
6x = 180°
x = 180° : 6 = 30° - это угол ∠1
2x = 2*30° = 60° - это угол ∠2
3x = 3*30° = 90° - это угол ∠3
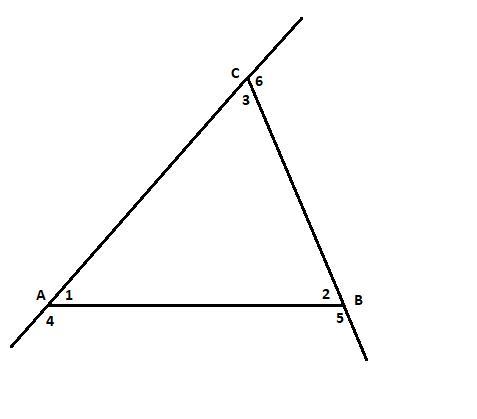
б) Сумма внешнего и внутреннего углов равна 180°
∠1 + ∠4 = ∠2 + ∠5 = ∠3 + ∠6 = 180°
∠5 = 180° - ∠2
∠6 = 180° - ∠3
По условию:
∠5 + ∠6 = 120°
180° - ∠2 + 180° - ∠3 = 120°
180° + 180° - 120° = ∠2 + ∠3
∠2 + ∠3 = 240°
Но ∠1 + ∠2 + ∠3 = 180°, поэтому ∠2 + ∠3 не может быть равно 240°.
В задаче опечатка.
Приложения:
Новые вопросы
Английский язык,
1 год назад
Другие предметы,
1 год назад
Физика,
6 лет назад
Математика,
8 лет назад
Математика,
8 лет назад