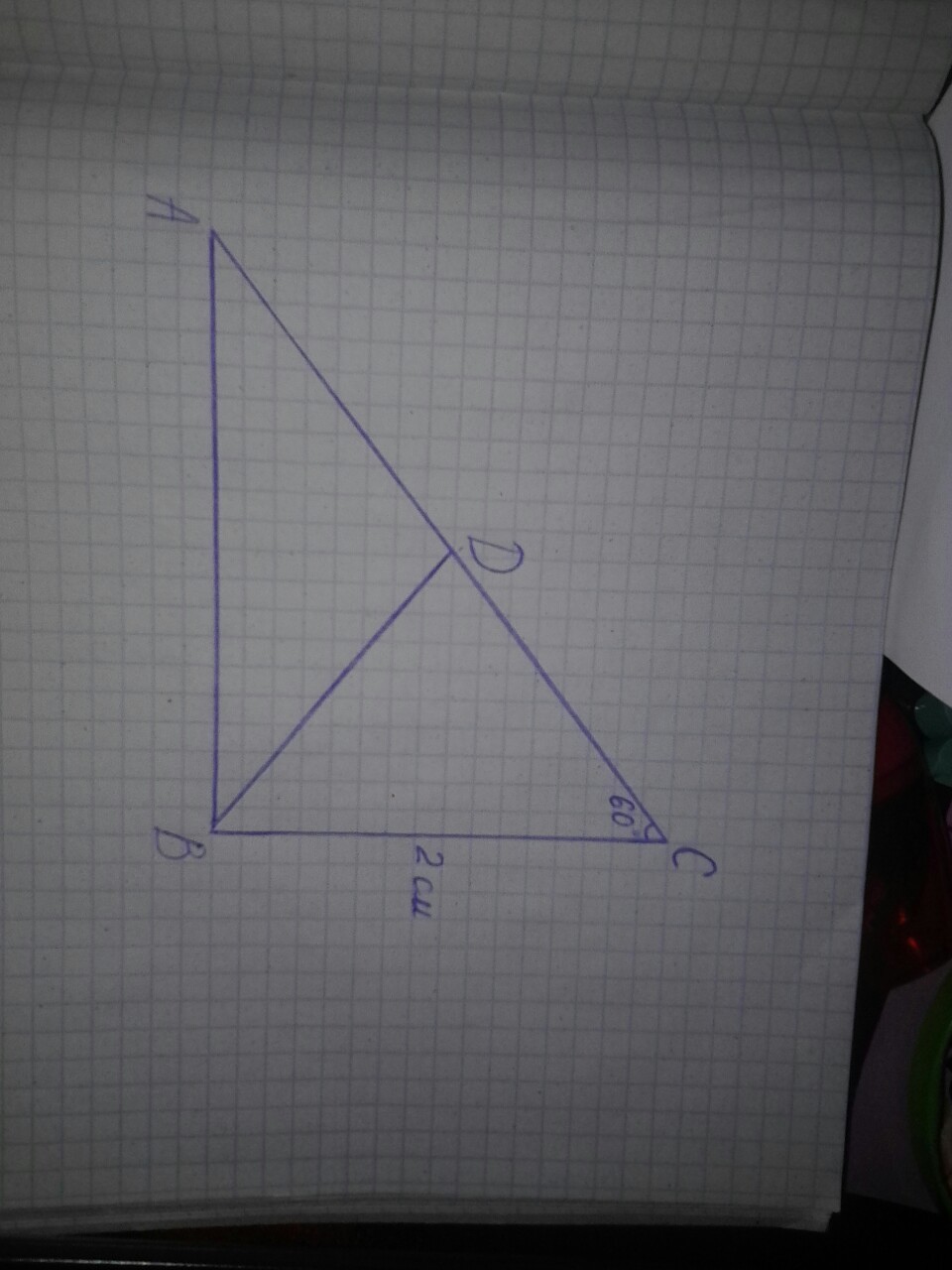
В треугольника АВС угол В равен 90 градусов, угол С равен 60 градусов, ВС равен 2 см. на стороне АС отмечена точка В так, что угол АВD равен 30 градусам. найдите длинну отрезка АD.

Решите пожалуйста на листочке нужен и чертёж и решение дам очень много баллов

Дано: ΔABC, ∠ABC=90° , ∠AСB= 60° , ∠ АВD =30°, ВС=2см

Найти : АD

Решение:

∠DВС=∠ABC-∠ АВD=90-30=60°

Рассмотрим Δ ВСD. ∠AСB= 60° , ∠DВС=60°. Δ ВСD равносторонний.

DВ=2см.

  Δ АDВ – равнобедренный, так как  ∠DАВ =30 °=∠ АВD.

АD=2см.

Спасибо

В прямоугольном треугольнике АВС ∠А=90-∠С=90-60=30°.
Катет ВС лежит напротив угла в 30 °, значит он вдвое меньше гипотенузы. АС=ВС·2=4 см.

В тр-ке АВД ∠АВД=∠ВАД=30°, значит он равнобедренный. АД=ВД.

∠СВД=∠АВС-∠АВД=90-30=60°.

В тр-ке ВСД ∠СВД=∠ВСД=60°, значит он равнобедренный. ВД=СД.

АД=ВД=СД, АС=АД+СД ⇒ АД=АС/2=2 см - это ответ.