В треугольник АВС вписана окружность, и к ней проведена касательная, пересекающая сторону АВ в точке К, а сторону ВС в точке М. Известно, что АК = 3, КМ = 2, МС = 4. Найдите периметр четырехугольника АКМС.
Ответы на вопрос
Ответил Беня2018
0
обозначим точки касания F Q D E соединим их с центром окружности а также соединим вершины искомого четырехугольника с центром окружности
так как касательная перпендикулярна точке касания получим равные прямоугольные треугольники по гипотенузе которая является общей стороной и катету который является радиусу окружности
ΔAFO=ΔOEA ; FKO=KOQ; QMO=MDO;DOC=COE
обозначим соответственно равные стороны этих треугольников через a b c d
получим
a+b=AK=3
c+d=MC=4
PAKMC=2a+2b+2c+2d=2(a+b)+2(c+d)=2*3+2*4=2(3+4)=14
Приложения:
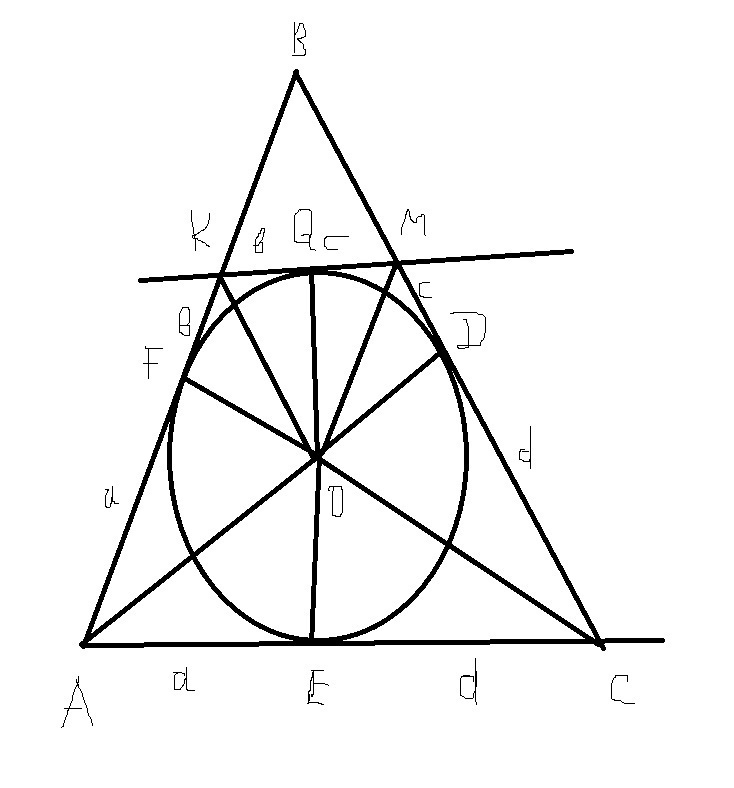
Новые вопросы