В трапеции известны длины диагоналей ac = 7, bd = 24, а также длина средней линии - 12,5. Найдите высоту трапеции
Ответы на вопрос
Ответил orjabinina
1
Объяснение:
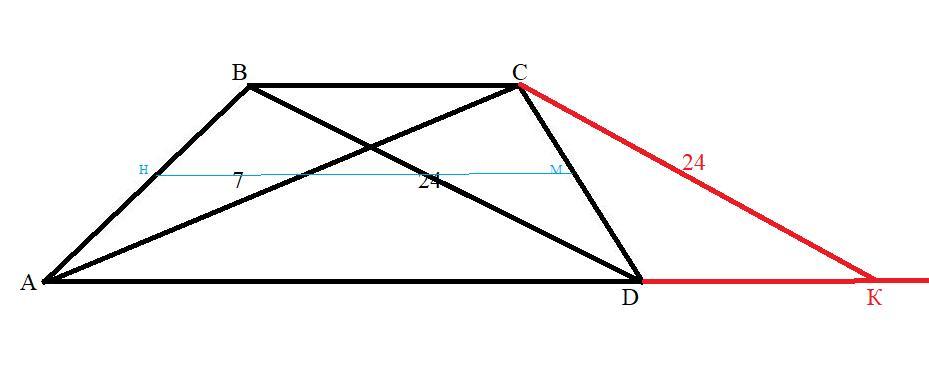
Дополнительные построения :пусть СО⊥АD , СК║ВD.
Тогда DВСК- параллелограмм , по определению , т.к. DК это продолжение стороны AD║ВС, и СК║ВD. Значит СК= ВD=24.
НМ- средняя линия. По свойству средней линии НМ=1/2(АD+ ВС), но ВС=DК ( как противоположные стороны параллелограмма) ⇒
НМ=1/2(АD+ DК)⇒ НМ=1/2АК⇒ АК=2НМ или АК=2*12,5=25.
Δ АСК, находим площадь по формуле Герона: S = √(р(р-а)(р-в)(р-с)).
АС=7, СК=24, АК=25,
Р=7+24+25=56, р=28.
S = √(28(28-7)(28-24)(28-25))= √(28*21*4*3) =√7056=84.
С другой стороны эту же площадь можно найти по формуле S=1/2*а*
, где а=АК=25, h=СО. Получаем 84=1/2*25*СН, СО=6,72
Приложения:
Новые вопросы
Математика,
1 год назад
Литература,
1 год назад
Математика,
1 год назад
Математика,
1 год назад
Другие предметы,
6 лет назад