В трапеции АВСD меньшая диагональ ВD перпендикулярна основаниям АD и ВС, сумма острых углов А и С равно 90. Найдите площадь трапеции, если основания АD=2, ВС=18. желательно подробно, ибо в геометрии не шарю

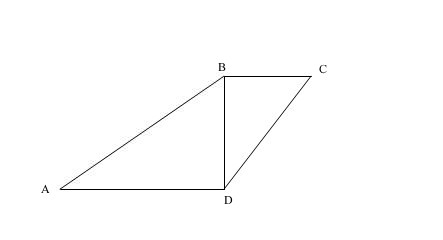
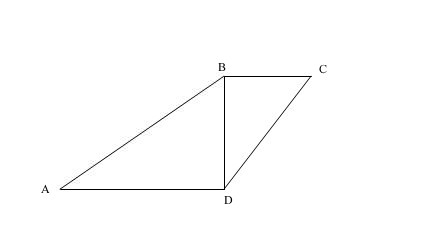
Дана трапеция ABCD. BD перп-на AD и BC.

Рассмотрим треугольник ADB - прямоугольный, следовательно, угол BAD + угол ABD = 90 гр.

По условию, угол А + угол С = 90 гр.

Если один из острых углов прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны.

Из подобия треугольников ABD и BCD:

AD:BD=DB:BC

18:BD=BD:2

BD^2 = 36

BD = 6

Sтрап = (ВС+AD)/2 * BD = (18+2)/2 * 6 = 60.