В трапеции ABCD (AD∥BC) ∠ABC=96∘ и ∠ADC=48∘ На луче BA за точкой A отметили точку K такую, что AK=BC . Найдите угол DKC, если известно, что ∠BKC=24∘.​

Ответ:

60градусов

Объяснение:

Сначала мы находим угол BCD. Этот угол равен 132градуса(по свойству о параллельных прямых).

Потом мы ищем угол BCK. Этот угол равен 60 градусов (по свойству о сумме углов треугольника).Затем мы ищем угол DCK. Этот угол равен 72 градуса .Так как 132-60.Потом мы ищем угол СKD.Этот угол равен 60 градусов (по свойству о сумме углов треугольника)

Ответ:

∠DKC = 36°.

Объяснение:

Вот один из вариантов решения:

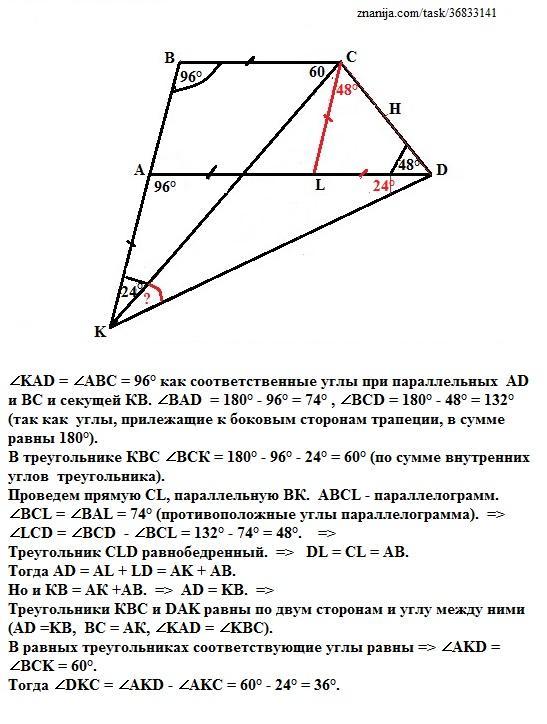
∠KAD = ∠ABC = 96° как соответственные углы при параллельных AD и ВС и секущей КВ. ∠BAD  = 180° - 96° = 74° , ∠BCD = 180° - 48° = 132° (так как углы, прилежащие к боковым сторонам трапеции, в сумме равны 180°).

В треугольнике КВС ∠ВСК = 180° - 96° - 24° = 60° (по сумме внутренних углов треугольника).

Проведем прямую СL, параллельную ВК.  АВСL - параллелограмм.

∠BCL = ∠BAL = 74° (противоположные углы параллелограмма).  =>

∠LСD = ∠BCD  - ∠BCL = 132° - 74° = 48°.    =>

Треугольник СLD равнобедренный.  =>   DL = CL = AB.

Тогда AD = AL + LD = AK + AB.

Но и КВ = АК +AВ.  =>  AD = KB.  =>  

Треугольники КВС и DAK равны по двум сторонам и углу между ними (AD =KB, BC = АК, ∠KAD = ∠KBC).

В равных треугольниках соответствующие углы равны => ∠AKD = ∠BCK = 60°.

Тогда ∠DKC = ∠AKD - ∠AKC = 60° - 24° = 36°.