В тра­пе­ции ABCD с ос­но­ва­ни­я­ми AD и BC диа­го­на­ли пе­ре­се­ка­ют­ся в точке O. До­ка­жи­те, что пло­ща­ди тре­уголь­ни­ков AOB и COD равны​

Ответ:

Доказательство в объяснении и приложении.

Объяснение:

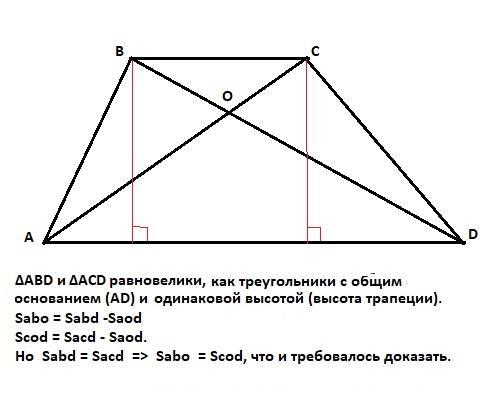
ΔABD и ΔАСD равновелики, то есть площади этих треугольников равны (Sabd = Sacd),так как эти треугольники с общим основанием (AD) и одинаковой высотой (высота трапеции). С другой стороны, площади этих треугольников равны разности:

Sabo = Sabd -Saod

Scod = Sacd - Saod.

Но  Sabd = Sacd  =>  

Sabo  = Scod, что и требовалось доказать.