В тетраэдре DABC построить сечение плоскостью, проходящей через
вершину А, точку М ребра DB, параллельной прямой ВС.

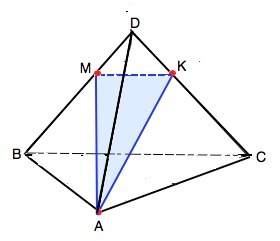
 На грани АВD расположены две точки искомого сечения - т.А и т.М. Соединив их, получим линию пересечения грани и плоскости сечения. 
 Так как плоскость сечения должна быть параллельна прямой ВС, то линия пересечения плоскости сечения и плоскости грани BDC будут параллельны. Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек.

По теореме:. Если прямая (ВС), не лежащая в данной плоскости (сечения), параллельна какой-нибудь прямой (МК), лежащей в этой плоскости, то она параллельна самой плоскости. Проведем МК║ВС и получим линию пересечения плоскостей грани и сечения. 

 На грани АDC теперь есть вторая точка, принадлежащая линии пересечения плоскости сечения и грани. Соединим их. 
АМК - искомое сечение.