Геометрия, вопрос задал KROSH148 , 2 года назад

В ромбе один из углов равен 60°. Меньшая диагональ равна 12 см. Найдите площадь ромба.

Аноним: При градусах 60°;120° диагональ равна стороне ромба. S=12²*sin60°=144*1/2=72см

KROSH148: без синуса можно пожалуйста?

Аноним: Теорема Пифагора √(12²-6²)=6√3; 6√3*2=12√3 вторая диагональ. S=1/2*d1*d2=1/2*12√3*12=72√3

Аноним: Ошиблась в первый раз.

KROSH148: СПАСИБО БОЛЬШОЕ

Аноним: Там в первом синус60=√3/2

Ответы на вопрос

Ответил alinochka2595

Стороны ромба равны, его диагонали взаимно перпендикулярны, точкой пересечения делятся пополам и являются биссектрисами углов ромба.
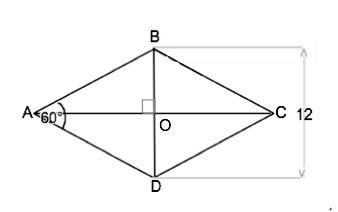
Обозначим ромб ABCD. BD и АС - диагонали.
Диагональ BD=12 см (дано).
∆ ВАD равнобедренный, угол ВАD=60° (дано), ⇒ углы при основании ВD равны 60°. ⇒ АВ=AD=ВD=12 см.
Диагональ АС=2АО.
АО=АВ•sin60°=6√3;
AC=12√3 см
-------
Как вариант для решения можно приметить т.Пифагора или теорему о равенстве суммы квадратов сторон и квадратов диагоналей параллелограмма.

Приложения: