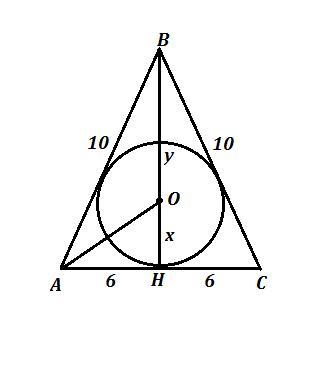В равнобедренный треугольник с основанием 12 см и периметром 32 см вписана окружность. Найдите радиус этой окружности.РЕШИТЕ НА ЛИСТОЧКЕ СРОЧНО ПОЖАЛУЙСТА ДАЮ 55 БАЛЛОВ СРОЧНО НУЖНО ПОЖАЛУЙСТА.
Ответы на вопрос
Ответ:
3 сантиметра- радиус вписаной окружности

Ответ:
ΔАВС - равнобедренный , АВ=ВС , АС=12 см , Р=32 см .
Так как периметр Р=32 см , то на боковые стороны приходится 32-12=20 (см) . Значит одна боковая сторона равна 20:2=10 (см) , АВ=ВС=10 см .
Высота ВН, проведённая к основанию равнобедренного треугольника является и медианой и биссектрисой . Поэтому АН=СН=12:2=6 см .
∠АНВ=90° , АВ²=АН²+ВН² , 10²=6²+ВН² , ВН²=100-36=64 , ВН=8 см .
Центр вписанной окружности, точка О, лежит на пересечении биссектрис . Значит, от будет лежать на ВН , причём радиус вписанной окружности равен R=ОН .
Проведём в точку О из вершины А прямую. Она будет биссектрисой угла А , так как в точке О пересекаются биссектрисы .
Рассм. ΔАВН . АО - биссектриса. Обозначим ОН=х , ОВ=у , х+у=8 .
По свойству биссектрисы имеем ОН:АН=ОВ:АВ , х:6=у:10 ⇒ у=5х/3 ,
у=8-х=5х/3 , 24-3х=5х , 8х=24 , х=3 ⇒ ОН=3 см .
Радиус вписанной окр. R=3 см .