В равнобедренной трапеции угол при основании равен 60°. Боковая сторона равна 24. Сумма оснований равна 60. Найти меньшее основание.
Ответ округлить до десятых.​

Рассмотрим треугольник ABH, с проведённой высотой BH

Этот треугольник прямоугольный, так как высота создаёт угол в 90°

∠А=60° по условию, значит ⇒ ∠ABH=180°-90°-60°=30°

Против угла в 30° лежит катет, равный половине гипотенузы

Значит, сторона y=12

То же самое происходит с другим треугольником CDH1

Всё схоже, так как это равнобедренная трапеция, и эти треугольники равны по 2 признаку равенства треугольников (2 угла и сторона)

Остаётся составить уравнение и найти основания

x+12+12+x=60

2x=36

x=18

Наименьшее основание равно 18

Ответ: Меньшее основание равно 18

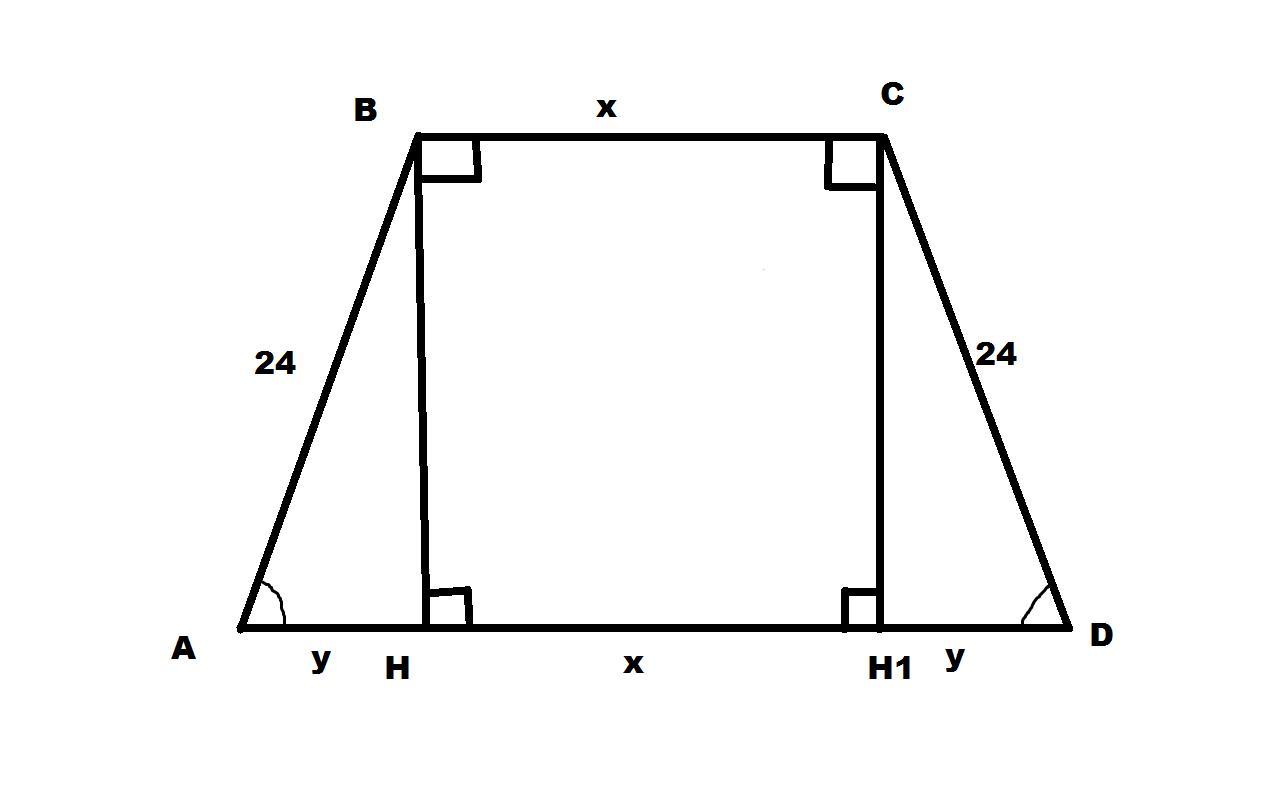
Проведём в р/б трапеции 2 высоты из точек верхнего основания на нижнее. Получается, что 180(сумма углов тр.)-90 (высота)-60(угол при основании тр.=30 градусов угол, а это значит что гипотенуза больше стороны лежащей напротив угла в 30 градусов в 2 раза, следовательно 24/2=12, но т.к. этих стороны 2(у нас 2 высоты разделили на 2 равных треугольника) будет 24 см. Далее составим решаем так:

60-24=36см -это у  нас 2 стороны квадрата, который образовался в ходе деления трапеции высотами (он разделился на 2 пр/уг треугольника и квадрат), следовательно эти стороны одинаковые 36/2=18см будет меньшее основание

смысл я так замудрёно написала, всё равно никто ничего не поймёт(