В равнобедренной трапеции диагональ является биссектрисой тупого угла. Найдите площадь трапеции, если боковая сторона равна 37 см, а меньшее основание 13см.

Ответ:

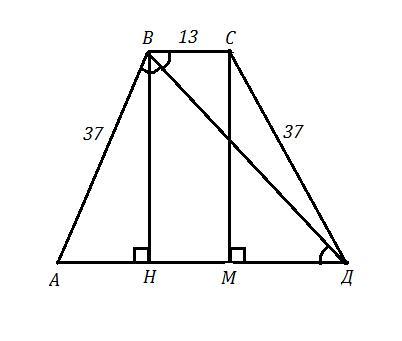
АВСД - трапеция  ,  АВ=СД=37 см ,  ВС=13 см , ВД - биссектриса ∠В .

 Так как ВД - биссектриса ∠В , то  ∠АВД=∠СВД .

Так как ВС║АД и ВД - секущая, то ∠СВД=∠АДВ как внутренние накрест лежащие углы, и тогда  ∠АВД=∠АДВ  ⇒   ΔАВД - равнобедренный, АВ=ВД=37 см .

 Проведём  ВН⊥АД и СМ⊥АД . ВСМН - прямоугольник и МН=ВС=13 см

АН=МД=37-13=24 см ,  АН=МД=24:2=12 см .

Рассмотрим ΔАВН .

По теореме Пифагора  ВН=√(АВ²-АН²)=√(37²-12²)=√1225=35 см .

ВН - высота трапеции.

Площадь трапеции:

S=(АД+BC)/2*ВН=(37+13)/2*35=50/2*35=25*35=875 см²