в равнобедренной трапеции диагональ перпендикулярна боковой стороне. найдите площадь трапеции, если большее основание равно 4корень3, а один из углов трапеции равен 60°.
П О Ж А Л У Й С Т А ! ​

Ответ:

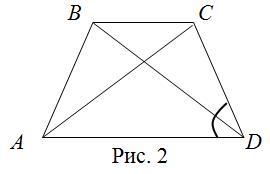
Дано . А, В, С, Д - вершины трапеции. АД = 4√3 см. ∠Д = 60°.

Найти. Площадь трапеции -?

АС : АД = синус 60°. АС = АД * √3/2 = 4√3 х √3/2 = 1,6 см.

∠САН. ∠САН = 180° - 90° - 60° = 30°.

СН : АС = синус 30°= 1/2.

СН = 1,6 * 1/2 = 0,5 см.

АН : АС = косинус ∠САН = косинус 30° = √3/2.

АН = АС х √3/2 =1,6 х √3/2= 4√3 /5см.

Согласно свойствам равнобедренной трапеции, (АД + ВС)/2 = АН = 4√3 /5см

Площадь трапеции = (ВС + АД)/2 х СН = = 4√3 /5 * 0,5  = 2√3/5 см².

Объяснение:

удачи вам :)