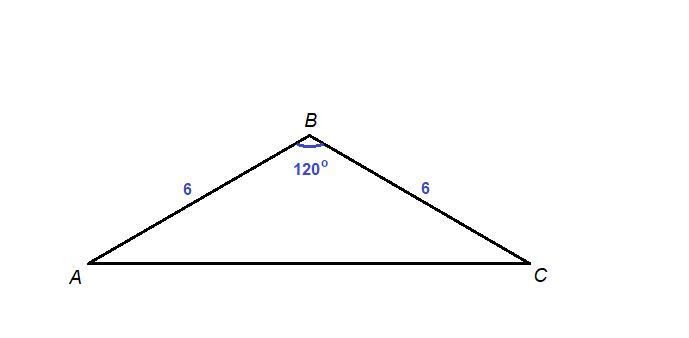
В равнобедренном треугольнике угол при вершине равен 120°, а боковая сторона – 6 см. Чему равен радиус окружности, описанной около данного треугольника?

R =см.

​

Ответ:

R = 6 см

Объяснение:

• Углы при основании равнобедренного треугольника равны.

• Сумма углов треугольника равна 180°.

∠А = ∠С = (180° - ∠В) : 2 = (180° - 120°) : 2 = 60° : 2 = 30°

По следствию из теоремы синусов:

• отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной окружности.

R = 12 : 2 = 6 см