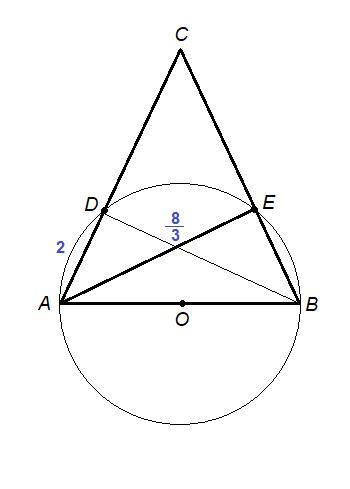
Геометрия, вопрос задал s0314254 , 6 лет назад

В равнобедренном треугольнике АВС на основании АВ как на диаметре построена окружность, которая пересекает боковые стороны АС и ВС в точках Д и Е соответственно. Причем АД = 2, АЕ = 8/3. Найдите периметр треугольника АВС. (запишите решение)

Ответы на вопрос

Ответил KuOV

Ответ:

$P=\dfrac{80}{9}$

Объяснение:

ΔDAB = ΔЕВА по гипотенузе и острому углу, ⇒

ВЕ = AD = 2

ΔАЕВ: ∠АЕВ = 90°, по теореме Пифагора

$\boldsymbol{AB}=\sqrt{AE^2+BE^2}=\sqrt{\left(\dfrac{8}{3}\right)^2+2^2}=$

$= \sqrt{\dfrac{64}{9}+4}=\sqrt{\dfrac{64+36}{9}}=\sqrt{\dfrac{100}{9}}\boldsymbol{=\dfrac{10}{3}}$

$\cos\angle ABE=\dfrac{BE}{AB}=2:\dfrac{10}{3}=2\cdot \dfrac{3}{10}=\dfrac{3}{5}$

АС = ВС = х

Из ΔАВС по теореме косинусов:

AC² = AB² + BC² - 2·AB·BC·cos∠ABE

$x^2=\left(\dfrac{10}{3}\right)^2+x^2-2\cdot \dfrac{10}{3}\cdot x\cdot \dfrac{3}{5}$

$x^2-x^2=\dfrac{100}{9}-2\cdot 2\cdot x$

$4x=\dfrac{100}{9}$

$x=\dfrac{25}{9}$

$AC = BC=\dfrac{25}{9}$

Периметр треугольника АВС:

$\boldsymbol{P}=AB+2\cdot AC=\dfrac{10}{3}+2\cdot \dfrac{25}{9}=\dfrac{30}{9}+\dfrac{50}{9}\boldsymbol{=\dfrac{80}{9}}$

Приложения:

Новые вопросы

Русский язык, 1 год назад

Немецкий язык, 1 год назад

Физика, 6 лет назад

Обществознание, 6 лет назад

Биология, 8 лет назад

Физика, 8 лет назад