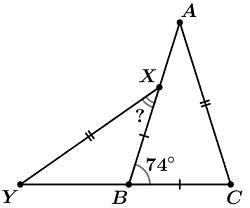
В равнобедренном треугольнике ABC с основанием BC на боковой стороне AB выбрана точка X так, что BX=BC, а на продолжении стороны BC за точку B выбрана такая точка Y, что XY=AC. Найдите угол YXB, если ∠B=74∘.

Продолжим отрезок AB за точку B. На продолжении отметим точку T так, что BT=YB. Получаем, что треугольники YBX и TBC равны по двум сторонам и углу между ними. Искомый угол YXB равен углу BCT. Сторона XY равна стороне CT. Значит, треугольник ACT равнобедренный. Угол T равен 32°, угол CBT равен 106°, а угол BCT равен 180°-32°-106°=42°. Значит, угол YBX равен 42°.