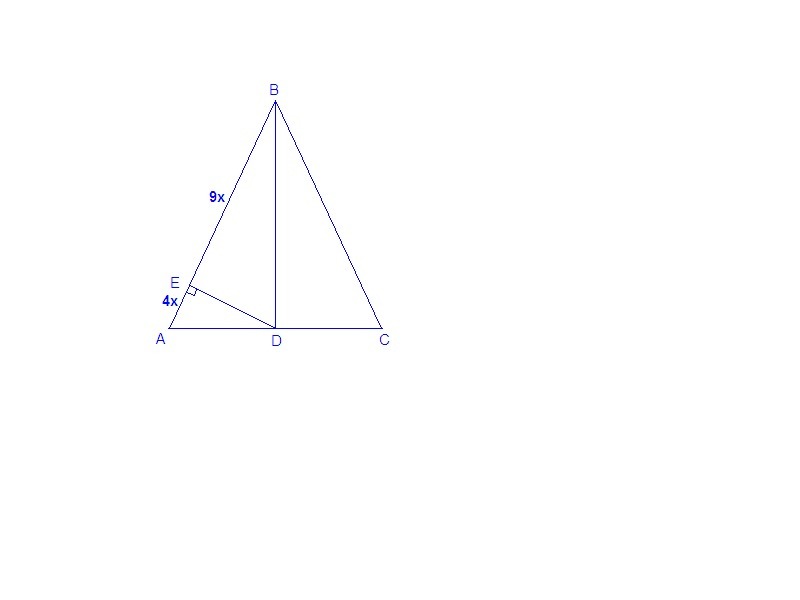
В равнобедренном треугольнике ABC AB=CB, BD-биссектриса, DE перпендикулярно AB, AE:BE=4:9, BD+AC=14см. Найти периметр ABC.
Ответы на вопрос
Ответил KuOV
0
Треугольник АВС равнобедренный, значит BD биссектриса, медиана и высота, т.е. AD = DC и ΔABD прямоугольный, а DE - его высота.
По свойству пропорциональных отрезков в прямоугольном треугольнике, квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу:
BD² = BE · AB
AD² = AE · AB
Пусть х - коэффициент пропорциональности, тогда
АЕ = 4х, ВЕ = 9х, а АВ = 13х.
BD = √(9х · 13х) = 3х√13
AD = √(4x · 13x) = 2x√13
AC = 2AD = 4x√13.
Так как BD + AC = 14, то
3x√13 + 4x√13 = 14
7x√13 = 14
x = 2/√13 = 2√13 / 13 см
AB = BC = 13x = 2√13 см
AC = 4x√13 = 4 · 2√13/13 · √13 = 8 см
Pabc = AB + BC + AC = 2AB + AC = 2 · 2√13 + 8 = 4(√13 + 2) см
Приложения:
Новые вопросы