в равнгбедреннной трапеции диагональ перпендикулярна боковой стороне. Найдитеплощадь трапеции, если большее основание равно 16 корню из 3, а один из углов трапеции равен 60градусов. Задание 5. 35 баллов
Приложения:

Ответы на вопрос
Ответил Пеппер
0
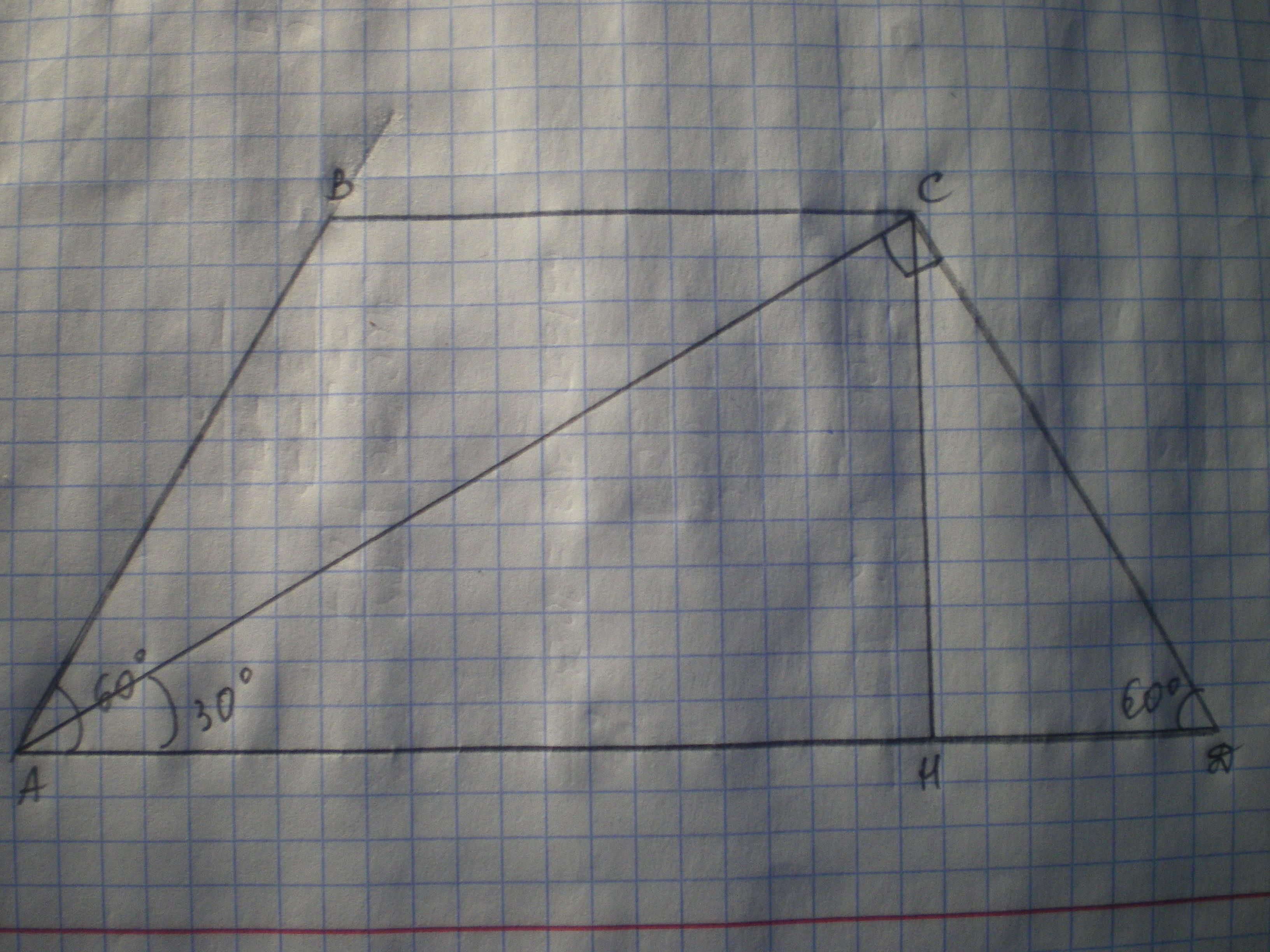
Дано: АВСД - трапеция, АВ=СД, АД=16√3, ∠А=∠Д=60°, АС⊥СД. Найти S(АВСД).
Решение: Проведем высоту СН, тогда S(АВСД)=(ВС+АД):2*СН.
Рассмотрим ΔАСД - прямоугольный, ∠Д=60°, тогда ∠САД=90-60=30°, а СД=12 АД=16√3:2=8√3.
Диагональ АС перпендикулярна к боковой стороне и делит угол А пополам, значит большее основание трапеции в два раза больше меньшего основания и её боковых сторон; и высота трапеции равна половине её диагонали.
СД=ВС=16√3:2=8√3;
АС²=(16√3)²-(8√3)²=768-192=576; АС=√576=24.
СН=12 АС=24:2=12.
S(АВСД)=(8√3+16√3):2*12=144√3 (ед²).
Ответ: 144√3 ед²
Приложения:
Новые вопросы