В прямоугольной трапеции диагональ является биссектрисой острого угла найдите площадь трапеции если боковые сторрны равны 6см и 10см

Ответ:

84 см²

Пошаговое объяснение:

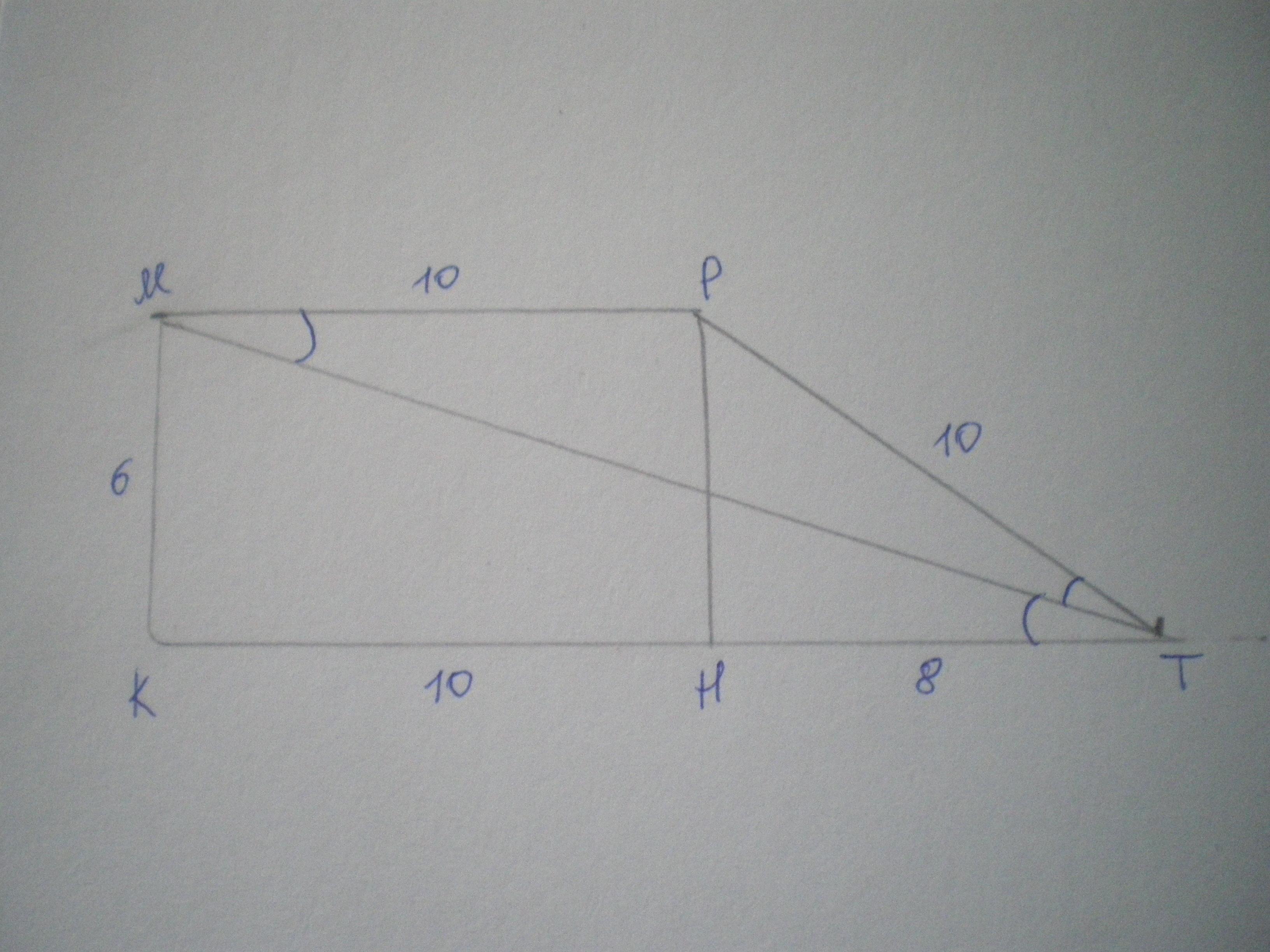
Дано: КМРТ - трапеция, ∠К=90°, МТ - биссектриса, МК=6 см, ТР=10 см. Найти S(КМРТ).

∠РМТ=∠МТК как накрест лежащие при МР║КТ и секущей МТ,  ∠РТМ=∠МТК по определению биссектрисы, тогда ΔМРТ - равнобедренный и МР=РТ=10 см.

Проведем высоту РН=МК=6 см.

Рассмотрим ΔРНТ - прямоугольный.

РН=6 см, РТ=10 см, значит, ТН=8 см ("египетский треугольник").

КН=МР=10 см; КТ=КН+ТН=10+8=18 см.

S=1/2 (МР+КТ) * РН = 1/2 * 28 * 6 = 84 см²