В прямоугольной трапеции ABCD с большим основанием AD и прямыми углами C и D меньшая диагональ BD является биссектрисой угла B и образует с боковой стороной AB угол 55°. Найдите угол между диагональю BD и боковой стороной, перпендикулярной основанию.
Ответы на вопрос
Ответил ludmilaksenija2005
6
Пошаговое объяснение:
Возьмём Треуг ВСD
<C=90
<DBC=<ABD=55 т. к биссектриса
<ВDC=180-(90+55)=180-145=35
LEXA21323:
спасибо
Ответил DenisPM
3
Дано:
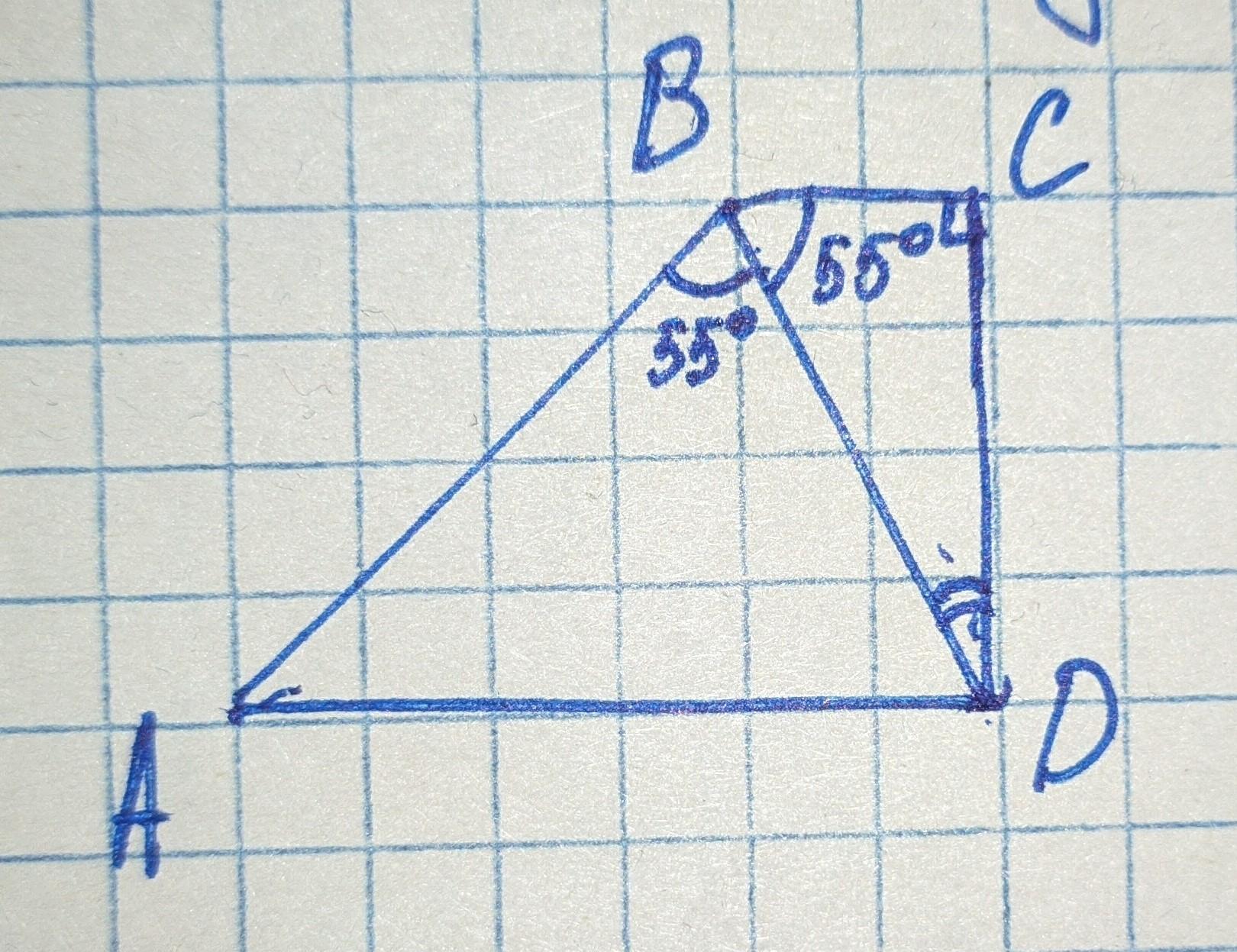
ABCD (рисунок прикреплён) - прямоуг. трапеция
∠C = ∠D = 90°
BD - биссектриса ∠B
∠ABD = 55°
AD - бОльшая сторона
Найти:
∠BDC = ?
Решение:
Так как BD - биссектриса ∠ABC, то ∠ABD = ∠ DBC = 55°.
Из ΔBCD:
∠BDC = 180° - ∠DBC - ∠BCD = 180° - 55° - 90° = 35°
Ответ: 35°.
Приложения:
Новые вопросы