В прямоугольном треугольнике угол между
высотой и биссектрисой, проведёнными из вершины
прямого угла, равен 20°. Найдите больший угол прямоугольного треугольника.
Ответ дайте в градусах.
Приложения:
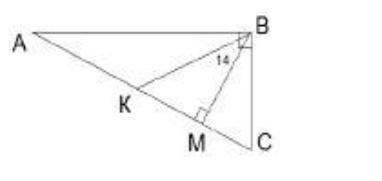
KBM=20 , а не 14. 14 у него отмечено на рисунке, но в условии 20.
Верно....
Ответы на вопрос
Ответил liftec74
2
Ответ: ∡C=65°
Объяснение:
Заметим , что в ΔВМС и ΔАВС угол ∡С- общий, а углы ∡АВС=∡ВМС=90°.
Тогда ∡СВМ=∡ВАС
Так как ВК- биссектриса, то ∡КВС=45° => ∡CBM=∡KBC-∡KBM=45°-20°=25° => ∡BAC=25°
=> ∡C=90°-∡BAC=90°-25°=65°
Новые вопросы
Литература,
11 месяцев назад
Математика,
11 месяцев назад
География,
1 год назад
Русский язык,
1 год назад
∆ВКМ, <ВКМ=90-14=76
∆АВК, по т о внешнем угле треугольника имеем <А+<АВК=76=>
<А=76-45=