В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла равен 34°. Найдите меньший угол данного треугольника.
Ответы на вопрос
Ответил KuOV
0
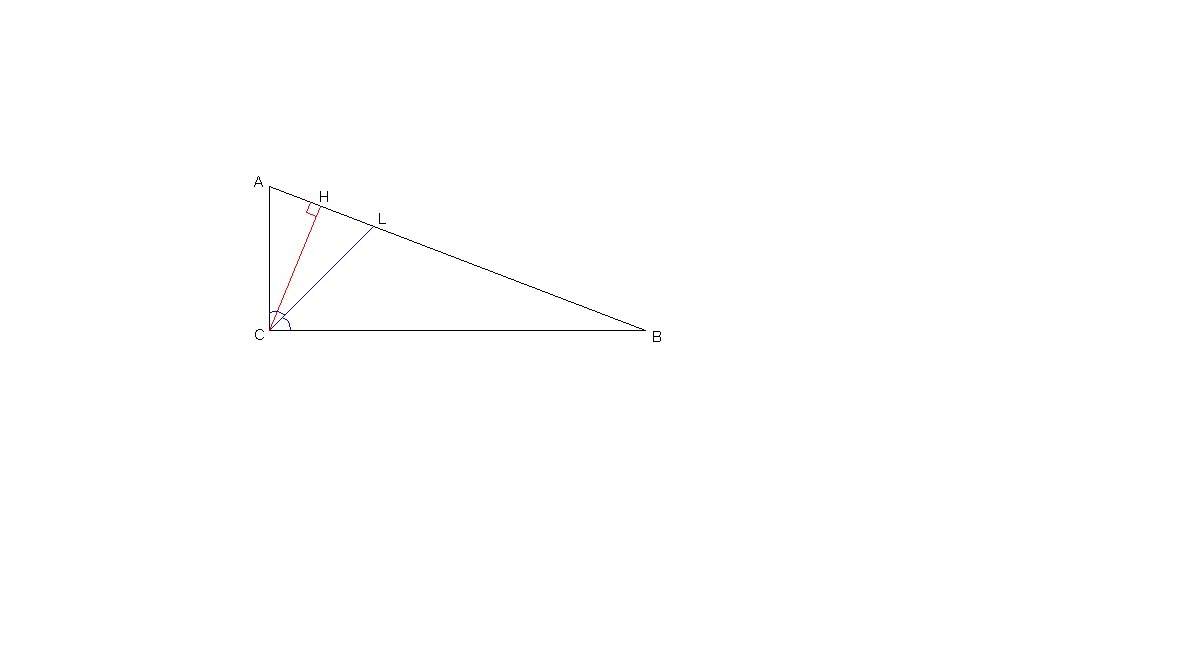
∠HCL = 34° по условию,
∠ACL = 45°, так как CL - биссектриса прямого угла,
∠АСН = ∠ACL - ∠HCL = 45° - 34° = 11°
ΔАСН: ∠Н = 90°, ∠С = 11°, ⇒ ∠А = 79°.
ΔАВС: ∠С = 90°, ∠А = 79°, ⇒ ∠В = 11°
∠ACL = 45°, так как CL - биссектриса прямого угла,
∠АСН = ∠ACL - ∠HCL = 45° - 34° = 11°
ΔАСН: ∠Н = 90°, ∠С = 11°, ⇒ ∠А = 79°.
ΔАВС: ∠С = 90°, ∠А = 79°, ⇒ ∠В = 11°
Приложения:
Новые вопросы