в прямоугольном треугольнике один из углов равен 30°, а катет прилежащий к нему равен 4, найдите площадь треугольника

с объяснением, пожалуйста​

Ответ:

  (ед²)

Объяснение:

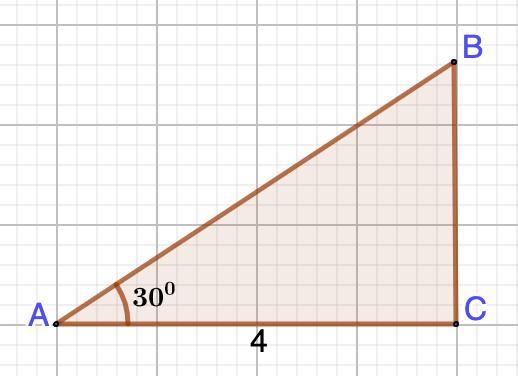
Дано: ΔАВС - прямоугольный;

∠А = 30°; АС = 4.

Найти: S ΔАВС.

Решение:

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ АВ = 2ВС

Пусть ВС = х, тогда АВ = 2х

По теореме Пифагора:

⇒

• Площадь прямоугольного треугольника равна половине произведения катетов.