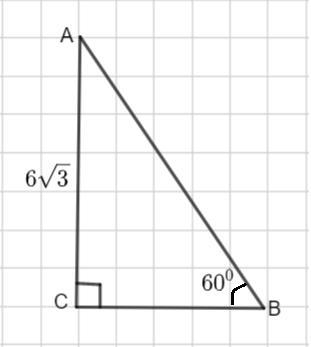
Геометрия, вопрос задал zilolasaripova48 , 2 года назад

в прямоугольном треугольнике один из катетов равен 6 корней из 3 а противолежащий угол равен 60 градусов Найдите гипотенузу и второй катет
срочно

Ответы на вопрос

Ответил lilyatomach

Ответ:

12 ед.- гипотенуза, а катет - 6 ед.

Объяснение:

Пусть дан Δ АВС - прямоугольный.

∠В=60°, АС=6√3 ед.

Сумма острых углов прямоугольного треугольника равна 90°.

Тогда ∠ А= 90°-60°=30°.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

$sin B= \dfrac{AC}{AB} ;\\\\sin60^{0} =\dfrac{6\sqrt{3} }{AB} ;\\\\\dfrac{\sqrt{3} }{2} =\dfrac{6\sqrt{3} }{AB};\\\\AB= \dfrac{6\sqrt{3} \cdot 2}{\sqrt{3} } =12$

Тогда гипотенуза АВ = 12 ед.

Найдем катет ВС по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB^{2} =AC^{2} +BC^{2} ;\\BC^{2}=AB^{2} -AC^{2};\\BC= \sqrt{AB^{2} -AC^{2}} ;\\BC= \sqrt{12^{2} -(6\sqrt{3})^{2} } =\sqrt{144-36\cdot3} =\sqrt{144-108} =\sqrt{36} =6$