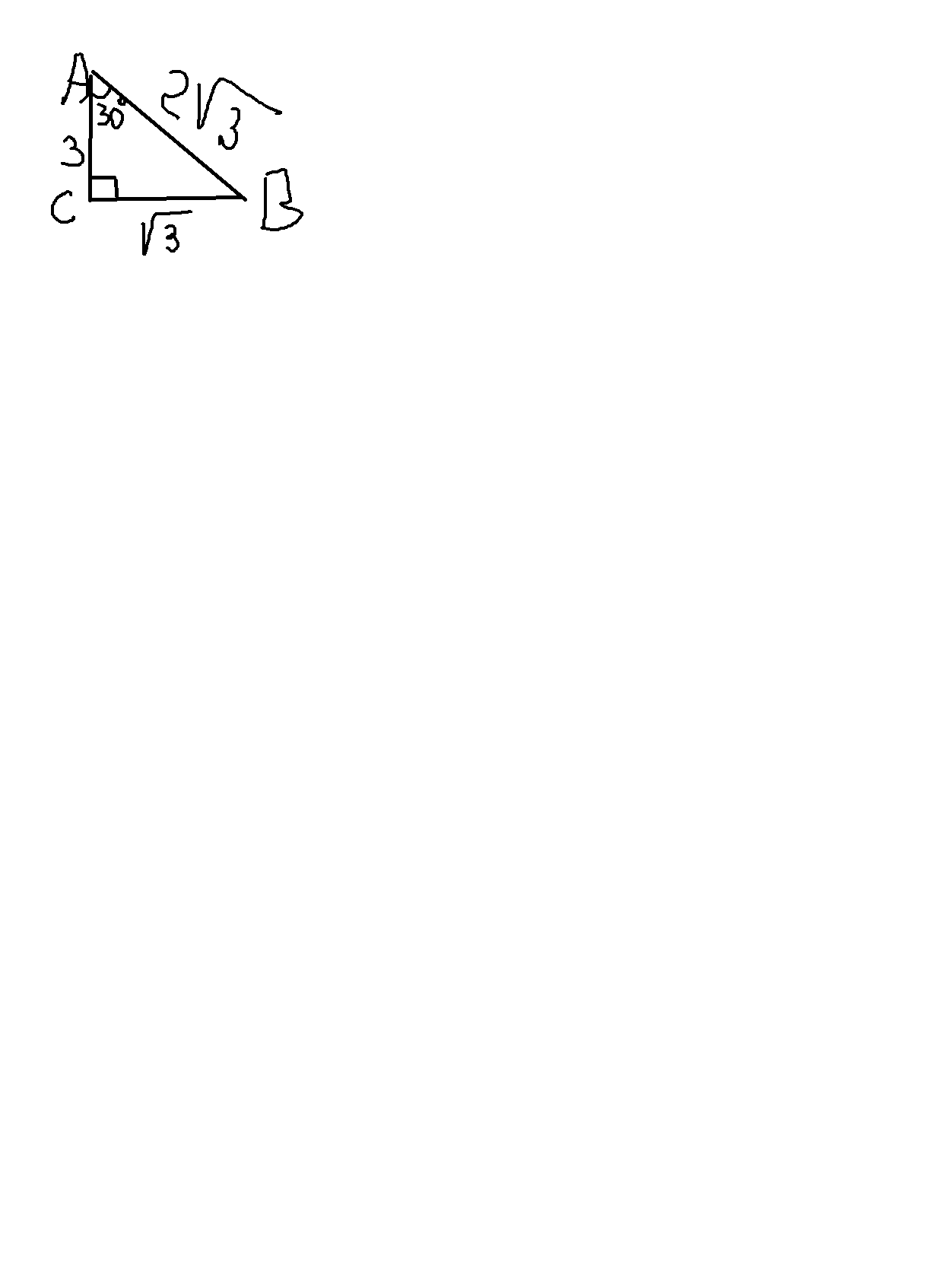
в прямоугольном треугольнике гипотенуза равна 2 корень из 3, а один из углов 30 градусов. Найдите площадь этого треугольника

гипотенуза=
угол А=30 градусов
Правило: Напротив угла в 30 гр. лежит катет равный половине гипотенузы.
Следовательно СВ= = 
Потом нужно найти второй катет(первый-СВ)
По теореме Пифагора:
где  - гипотенуза ; а и b - катеты

следовательно



AC=3
Площадь прям.треугольника находится по формуле:
где a и b - катеты  

С последним не уверена (так как там ещё можно занести под корень 3 и делить :()Это моё мнение .Решать тебе что писать.ФОРМУЛА ТОЧНАЯ!